SURF, Fresco e Natural
Enunciado
Uma nova empresa de refrigerantes pretende lançar no mercado embalagens de sumo de fruta, com capacidade de dois litros.
Por questões de marketing, as embalagens deverão ter a forma de um prisma quadrangular regular.
- Mostre que a área total da embalagem, em dm2, é dada por \[A(x)=2{{x}^{2}}+\frac{8}{x}\]
(x é o comprimento da aresta da base, em dm)
Nota: Recorde que $1\ litro=1\ d{{m}^{3}}$. - Utilizando métodos exclusivamente analíticos, mostre que existe um valor de x para o qual a área total da embalagem é mínima e determine-o.
- Há exatamente dois valores de x para os quais a área total da embalagem é igual a 12 dm2.
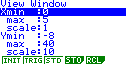
Recorrendo à sua calculadora, resolva graficamente este problema.
Apresente as soluções com aproximação às décimas. Explique como procedeu, apresentando o gráfico, ou gráficos, em que se baseou para dar a sua resposta.
Resolução
- A área de uma das bases do prisma é ${{A}_{b}}={{x}^{2}}$ e a altura do prisma é $h=\frac{2}{{{x}^{2}}}$, pois o seu volume é 2.
Logo, a área de uma das faces laterais é ${{A}_{fL}}=x.\frac{2}{{{x}^{2}}}=\frac{2}{x}$.
Assim, \[A(x)=2\times {{x}^{2}}+4\times \frac{2}{x}=2{{x}^{2}}+\frac{8}{x}\] para $x>0$.
- Ora, \[A'(x)=4x-\frac{8}{{{x}^{2}}}=\frac{4{{x}^{3}}-8}{{{x}^{2}}}=\frac{4.({{x}^{3}}-2)}{{{x}^{2}}}\] para $x>0$.
Como ${{x}^{3}}-2=0\Leftrightarrow x=\sqrt[3]{2}$, vem:
$x$ $0$ $\sqrt[3]{2}$ $+\infty $ $4.({{x}^{3}}-2)$ – – $0$ + ${{x}^{2}}$ $0$ + + + $A'(x)$ n.d. – $0$ + $A(x)$ n.d. $\searrow $ $A(\sqrt[3]{2})$ $\nearrow $ Portanto, o valor de x para o qual a área total da embalagem é mínima é $\sqrt[3]{2}$.
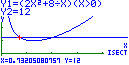
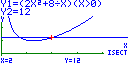
- As soluções do problema são as abcissas dos pontos de intersecção do gráfico da função A com a reta de equação $y=12$. Com recurso à calculadora, podemos obter parte do gráfico da função A, parte da reta de equação $y=12$, bem como as abcissas dos pontos de intersecção do gráfico da função com a referida reta:
As solução do problema, com aproximação às décimas, são $0,7$ e $2,0$.
