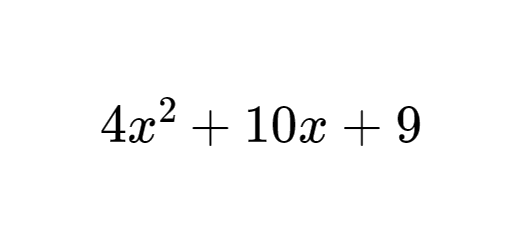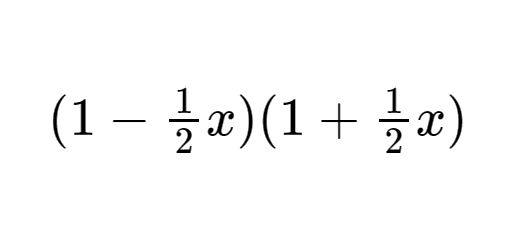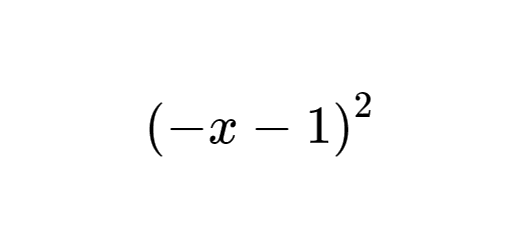Category: Equações de grau superior ao 1.º
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 81 Ex. 9
Enunciado
Resolve as seguintes equações:
- $x(x-1)=0$
- $(a-1)(a+1)=0$
- ${{x}^{2}}-2x=0$
- ${{a}^{2}}-6a+9=0$
- $4{{y}^{2}}+25=20y$
- ${{c}^{2}}-0,25=0$
- $0,04{{x}^{2}}-0,4x+1=0$
- ${{x}^{2}}=0,01$
Resolução >>
Resolução
-
\[\begin{array}{*{35}{l}}
x(x-1)=0 & \Leftrightarrow & \begin{array}{*{35}{l}}
x=0 & \vee & x-1=0 \\
\end{array} \\
{} & \Leftrightarrow & \begin{array}{*{35}{l}}
x=0 & \vee & x=1 \\
\end{array} \\
\end{array}\]
-
\[\begin{array}{*{35}{l}}
(a-1)(a+1)=0 & \Leftrightarrow
…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 78 Ex. 23
Enunciado
Determina o conjunto-solução de cada uma das equações:
- ${{x}^{2}}-6x+9=0$
- ${{x}^{3}}-2{{x}^{2}}+x=0$
- ${{x}^{2}}-16=0$
- $x({{x}^{2}}-25)=0$
- $8{{x}^{3}}-2x=0$
- $4{{x}^{2}}+4x+1=0$
- ${{x}^{2}}-36=0$
- ${{x}^{2}}-{{(3x+1)}^{2}}=0$
- ${{(x+1)}^{2}}-(x+1)=0$
Resolução >>
Resolução
-
\[\begin{array}{*{35}{l}}
{{x}^{2}}-6x+9=0 & \Leftrightarrow & {{(x-3)}^{2}}=0 \\
{} & \Leftrightarrow & (x-3)=0 \\
{} & \Leftrightarrow & x=3 \\
\end{array}\]
Portanto, o conjunto-solução da equação é $S=\left\{
…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 77 Ex. 22
Enunciado
Resolve as equações, utilizando a lei do anulamento do produto:
- $x(x+2)=0$
- $(2x+1)(x-\frac{1}{3})=0$
- ${{x}^{2}}+3x=0$
- $3{{z}^{2}}-12z=0$
- $(x-3)(2+7x)=0$
- $x(x+1)+2(x+1)=0$
- $-x(x+4)=0$
- $(x+4)x-3(x+4)=0$
- $3(x-2)(x+2)=0$
- $16x+2{{x}^{2}}=0$
- $2{{m}^{2}}+5m=0$
Resolução >>
Resolução
Lei do anulamento do produto
Um produto é nulo se e só se pelo menos um dos factores for nulo.
$\begin{matrix}
A\times B=0
…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 75 Ex. 21
Será possível factorizar o trinómio $4{{x}^{2}}+10x+9$ ?
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 75 Ex. 20
Enunciado
Decompõe em factores os polinómios:
- ${{x}^{2}}-6x+9$
- $4{{x}^{2}}+4x+1$
- ${{a}^{2}}+2ab+{{b}^{2}}$
- ${{y}^{2}}-25$
- $4{{a}^{2}}-1$
- $8{{x}^{3}}y-2x{{y}^{3}}$
- $2{{x}^{2}}+12x+18$
- $3{{a}^{2}}x+6ax+3x$
- ${{x}^{3}}-x$
- ${{a}^{2}}(a-2)-2a(a-2)+(a-2)$
Resolução >>
Resolução
-
$\begin{array}{*{35}{l}}
{{x}^{2}}-6x+9 & = & {{(x-3)}^{2}} \\
{} & = & (x-3)(x-3) \\
\end{array}$
-
$\begin{array}{*{35}{l}}
4{{x}^{2}}+4x+1 & = & {{(2x+1)}^{2}} \\
{} & = & (2x+1)(2x+1) \\
\end{array}$
-
$\begin{array}{*{35}{l}}
…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 74 Ex. 19
Enunciado
Transforma as seguintes expressões em produtos, colocando os factores comuns em evidência:
- $mx+nx$
- $6+3x$
- $4a-8$
- $5x-10{{x}^{2}}$
- $8{{x}^{2}}+2x-4$
- $5{{a}^{3}}-15{{a}^{2}}+5a$
- $\frac{1}{5}{{x}^{3}}-3{{x}^{2}}$
- $3(x-5)+x(x-5)$
- $\frac{1}{2}(x-2)+(x-2)x$
- ${{(x+7)}^{2}}-(x+7)$
- ${{(x-2)}^{2}}-2(x-2)$
- $6+2y+3x+xy$
Resolução >>
Resolução
-
$mx+nx=x(m+n)$
-
$6+3x=3(2+x)$
-
$4a-8=4(a-2)$
-
$5x-10{{x}^{2}}=5x(1-2x)$
-
$8{{x}^{2}}+2x-4=2(4{{x}^{2}}+x-2)$
-
$5{{a}^{3}}-15{{a}^{2}}+5a=5a({{a}^{2}}-3a+1)$
-
$\frac{1}{5}{{x}^{3}}-3{{x}^{2}}={{x}^{2}}(\frac{1}{5}x-3)$
-
$3(x-5)+x(x-5)=(x-5)(3+x)$
-
$\frac{1}{2}(x-2)+(x-2)x=(x-2)(\frac{1}{2}+x)$
-
$\begin{array}{*{35}{l}}
{{(x+7)}^{2}}-(x+7) & = & (x+7)\left[ (x+7)-1 \right] \\
{} &
…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 81 Ex. 8
Enunciado
Calcula mentalmente: $\begin{matrix}
{{101}^{2}} & {} & {{99}^{2}} & {} & 49\times 51 \\
\end{matrix}$
Explica como procedeste.
Resolução >>
Resolução
\[\begin{array}{*{35}{l}}
{{101}^{2}} & = & {{(100+1)}^{2}} \\
{} & = & 10000+200+1 \\
{} & = & 10201 \\
\end{array}\]
\[\begin{array}{*{35}{l}}
{{99}^{2}} & = & {{(100-1)}^{2}} …
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 81 Ex. 7
Enunciado
Desenvolve e simplifica cada uma das seguintes expressões:
- $15x-{{(x+7)}^{2}}$
- $x(x-1)-{{(x-2)}^{2}}$
- $(x+2)(x-3)+{{(x+1)}^{2}}$
- ${{(x+\frac{1}{2})}^{2}}-{{(x-\frac{1}{2})}^{2}}-\frac{3}{4}(x-1)(x+1)$
Resolução >>
Resolução
-
\[\begin{array}{*{35}{l}}
15x-{{(x+7)}^{2}} & = & 15x-({{x}^{2}}+14x+49) \\
{} & = & 15x-{{x}^{2}}-14x-49 \\
{} & = & -{{x}^{2}}+x-49 \\
\end{array}\]
-
\[\begin{array}{*{35}{l}}
x(x-1)-{{(x-2)}^{2}} & = & {{x}^{2}}-x-({{x}^{2}}-4x+4) \\
{} & = & {{x}^{2}}-x-{{x}^{2}}+4x-4)
…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 71 Ex. 18
Enunciado
Completa:
- $(….+….)(2x-….)=….-9$
- $(4a+….)(….-….)=16{{a}^{2}}-25$
- $(….-x)(….+….)=4-{{x}^{2}}$
Resolução >>
Resolução
- $(….+….)(2x-….)=….-9$
$(2x+3)(2x-3)=4{{x}^{2}}-9$
- $(4a+….)(….-….)=16{{a}^{2}}-25$
$(4a+5)(4a-5)=16{{a}^{2}}-25$
- $(….-x)(….+….)=4-{{x}^{2}}$
$(2-x)(2+x)=4-{{x}^{2}}$
<< Enunciado…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 71 Ex. 17
Enunciado
Calcula:
- $(x+5)(x-5)$
- $(2x-1)(2x+1)$
- $(1-x)(1+x)$
- $(1-\frac{1}{2}x)(1+\frac{1}{2}x)$
- $(4xy-3)(4xy+3)$
Resolução >>
Resolução
-
\[\begin{array}{*{35}{l}}
(x+5)(x-5) & = & {{x}^{2}}-{{5}^{2}} \\
{} & = & {{x}^{2}}-25 \\
\end{array}\]
-
\[\begin{array}{*{35}{l}}
(2x-1)(2x+1) & = & {{(2x)}^{2}}-{{1}^{2}} \\
{} & = & 4{{x}^{2}}-1 \\
\end{array}\]
-
\[\begin{array}{*{35}{l}}
(1-x)(1+x) & = & {{1}^{2}}-{{x}^{2}} \\
{} & =
…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 70 Ex. 16
Enunciado
Completa:
- ${{(x+….)}^{2}}=….+8x+16$
- ${{(….+4)}^{2}}=9{{x}^{2}}+24x+….$
- ${{(5x-….)}^{2}}=….-….+9$
- ${{(….-….)}^{2}}={{x}^{2}}-2x+….$
Resolução >>
Resolução
- ${{(x+….)}^{2}}=….+8x+16$
${{(x+4)}^{2}}={{x}^{2}}+8x+16$
- ${{(….+4)}^{2}}=9{{x}^{2}}+24x+….$
${{(3x+4)}^{2}}=9{{x}^{2}}+24x+16$
- ${{(5x-….)}^{2}}=….-….+9$
${{(5x-3)}^{2}}=25{{x}^{2}}-30x+9$
- ${{(….-….)}^{2}}={{x}^{2}}-2x+….$
${{(x-1)}^{2}}={{x}^{2}}-2x+1$
<< Enunciado…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 70 Ex. 15
Enunciado
Calcula:
- ${{(2x-3)}^{2}}$
- ${{(x+7)}^{2}}$
- ${{\left( y+\frac{1}{2} \right)}^{2}}$
- ${{(4a-3b)}^{2}}$
- ${{(-x-1)}^{2}}$
- ${{(x+1)}^{2}}$
Resolução >>
Resolução
-
\[\begin{array}{*{35}{l}}
{{(2x-3)}^{2}} & = & {{(2x)}^{2}}+2\times 2x\times (-3)+{{(-3)}^{2}} \\
{} & = & 4{{x}^{2}}-12x+9 \\
\end{array}\]
-
\[\begin{array}{*{35}{l}}
{{(x+7)}^{2}} & = & {{x}^{2}}+2\times x\times 7+{{7}^{2}} \\
{} & = & {{x}^{2}}+14x+49 \\
\end{array}\]
-
\[\begin{array}{*{35}{l}}
{{\left( y+\frac{1}{2}
…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 81 Ex. 6
Enunciado
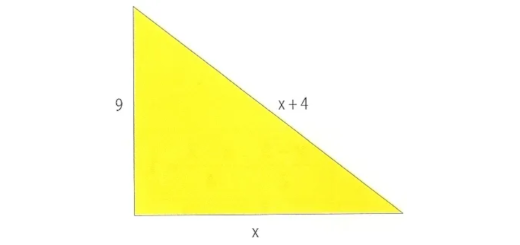
Determina o valor de x de modo que o triângulo seja rectângulo.
Resolução >>
Resolução
Para que o triângulo seja rectângulo terá de se verificar: ${{x}^{2}}+{{9}^{2}}={{(x+4)}^{2}}$. (Porquê?)
Assim, temos:
\[\begin{array}{*{35}{l}}
{{x}^{2}}+{{9}^{2}}={{(x+4)}^{2}} & \Leftrightarrow & {{x}^{2}}+81=(x+4)(x+4) \\
{} & \Leftrightarrow & {{x}^{2}}+81={{x}^{2}}+4x+4x+16 \\
{} & \Leftrightarrow & 8x=65 …
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 81 Ex. 5
Enunciado
Queremos dispor em forma de quadrado vários azulejos, de forma também quadrada.
Experimentámos de duas maneiras. Da primeira vez sobraram 39. Acrescentámos então mais um azulejo de cada lado. Desta vez faltaram 50.
De quantos azulejos dispúnhamos inicialmente?
Resolução >>
Resolução
Seja N o número de azulejos …
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 80 Ex. 4
Enunciado
Dados os polinómios:
| $A=2{{x}^{2}}-x-1$ |
$B=-3{{x}^{2}}+3x$ |
$C=4{{x}^{3}}-3$ |
$D=2x+6$ |
- Qual é o grau de cada um dos polinómios?
- Calcula, reduzindo os termos semelhantes:
- $A+B$
- $A+C+D$
- $2B-3D$
- $C\times D$
Resolução >>
Resolução
| $A=2{{x}^{2}}-x-1$ |
$B=-3{{x}^{2}}+3x$ |
$C=4{{x}^{3}}-3$ |
$D=2x+6$ |
- Os polinómios A e B são de grau 2, o polinómio C é de
…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 80 Ex. 3
Enunciado
Observa os rectângulos.
Calcula:
- a área de cada um dos rectângulos na forma reduzida;
- a diferença entre a área do rectângulo A e a área do rectângulo B.
Resolução >>
Resolução
- A área dos rectângulos pode ser expressa por:
$\begin{array}{*{35}{l}}
{{A}_{A}} & = & 0,5x\times 3y \\
…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 80 Ex. 2
Enunciado
Indica pares de monómios semelhantes:
| (I) |
(II) |
(III) |
(IV) |
(V) |
(VI) |
| $4x$ |
$8{{a}^{2}}$ |
$-2{{a}^{2}}x$ |
$3,4x$ |
${{a}^{2}}x$ |
${{a}^{2}}$ |
Resolução >>
Resolução
| (I) |
(II) |
(III) |
(IV) |
(V) |
(VI) |
| $4x$ |
$8{{a}^{2}}$ |
$-2{{a}^{2}}x$ |
$3,4x$ |
${{a}^{2}}x$ |
${{a}^{2}}$ |
São semelhantes os monómios: I e IV; II e VI; III e V.
<< …
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 80 Ex. 1
Completa o seguinte quadro:
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 67 Ex. 14
Calcula e simplifica:
$2x({{x}^{2}}+3x-\frac{1}{2})$
$-3x(-x+4)$
$({{x}^{2}}-7x)\times \frac{{{x}^{3}}}{2}$
$(n-2)(n+3)$
$(3a-1)({{a}^{2}}+\frac{1}{4})$
$(1-m-{{m}^{2}})(m+2)$
$(\frac{a}{2}-3)({{a}^{2}}-6a)$
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 66 Ex. 13
Enunciado
Calcula e simplifica:
- $3\times 5x$
- $2a\times (-a)$
- $-3yz\times \frac{1}{3}y$
- $-2{{x}^{2}}\times (-5{{x}^{3}})$
- $3{{a}^{2}}b\times \frac{ab}{3}$
- ${{({{x}^{2}}y)}^{2}}$
- ${{\left( -\frac{1}{2}m{{n}^{2}}p \right)}^{3}}$
Resolução >>
Resolução
- $3\times 5x=(3\times 5)\times x=15x$
- $2a\times (-a)=2\times (a\times (-a))=2\times (-{{a}^{2}})=-2{{a}^{2}}$
- $-3yz\times \frac{1}{3}y=(-3\times \frac{1}{3})\times (yz\times y)=-1\times {{y}^{2}}z=-{{y}^{2}}z$
- $-2{{x}^{2}}\times (-5{{x}^{3}})=(-2\times (-5))\times ({{x}^{2}}\times {{x}^{3}})=10\times {{x}^{5}}=10{{x}^{5}}$
- $3{{a}^{2}}b\times \frac{ab}{3}=(3\times \frac{1}{3})\times ({{a}^{2}}b\times ab)=1\times {{a}^{3}}{{b}^{2}}={{a}^{3}}{{b}^{2}}$
…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 66 Ex. 12
Considera a expressão: \[5{{x}^{3}}-(-3x)\times 2{{x}^{2}}-\frac{3}{2}{{x}^{4}}+\frac{3}{5}x+4\]
Transforma-a num polinómio reduzido e ordena-o.
Qual é o grau deste polinómio?
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 65 Ex. 11
Enunciado
Considera os polinómios:
| $A=7{{x}^{2}}-2x+\frac{1}{2}$ |
$B={{x}^{2}}-4x$ |
$C=3{{x}^{2}}-4x+\frac{7}{3}$ |
$D=3{{x}^{2}}+\frac{1}{2}x-\frac{2}{3}$ |
Determina e indica o grau de cada polinómio obtido:
- $A+B$
- $B-C$
- $C-D$
- $A-(B+C+D)$
Resolução >>
Resolução
| $A=7{{x}^{2}}-2x+\frac{1}{2}$ |
$B={{x}^{2}}-4x$ |
$C=3{{x}^{2}}-4x+\frac{7}{3}$ |
$D=3{{x}^{2}}+\frac{1}{2}x-\frac{2}{3}$ |
-
\[\begin{array}{*{35}{l}}
A+B & = & (7{{x}^{2}}-2x+\frac{1}{2})+({{x}^{2}}-4x) \\
{} & = & 7{{x}^{2}}+{{x}^{2}}-2x-4x+\frac{1}{2} \\
{} & = & 8{{x}^{2}}-6x+\frac{1}{2} \\
…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 64 Ex. 8
Enunciado
Considera as seguintes expressões:
| (I) |
(II) |
(III) |
(IV) |
(V) |
(VI) |
| $2x+3y$ |
$-\frac{5}{3}$ |
$a$ |
$\frac{3}{2}a$ |
$\frac{2}{3}+x$ |
$et$ |
- Indica as que são monómios.
- De entre os monómios da alínea anterior, indica os que são semelhantes.
Resolução >>
Resolução
| (I) |
(II) |
(III) |
(IV) |
(V) |
(VI) |
| $2x+3y$ |
$-\frac{5}{3}$ |
$a$ |
$\frac{3}{2}a$ |
$\frac{2}{3}+x$ |
…
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 64 Ex. 7
Enunciado
Copia e completa:
| Monómio |
Parte literal |
Coeficiente |
Grau |
| $3{{x}^{6}}$ |
|
|
|
| $-a$ |
|
|
|
| $\frac{x}{2}$ |
|
|
|
| $abc$ |
|
|
|
| $-2$ |
|
|
|
| $\frac{-y}{3}$ |
|
|
|
Resolução >>
Resolução
| Monómio |
Parte literal |
Coeficiente |
Grau |
| $3{{x}^{6}}$ |
${{x}^{6}}$ |
$3$ |
6 |
| $-a$ |
$a$ |
$-1$ |
1 |
| $\frac{x}{2}$ |
$x$ |
$\frac{1}{2}$ |
1 |
| $abc$ |
$abc$ |
$1$ |
3 |
| $-2$ |
—– |
$-2$ |
0 |
| $\frac{-y}{3}$ |
$y$ |
$-\frac{1}{3}$ |
1 |
…
Comentários recentes