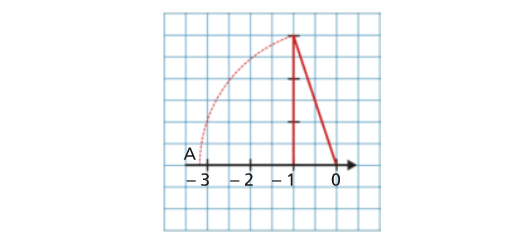
Copia e completa
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 71 Ex. 5
Copia e completa com o sinal < ou >, de modo a obteres afirmações verdadeiras.
| a) | b) | c) | d) |
| \( – 1,7 \ldots – 7\) | \(\pi \ldots \sqrt {17} \) | \( – \frac{8}{3} \ldots – 2,7\) | \(\sqrt 2 \ldots 1,41\) |
Resolução >> Resolução
<< Enunciado… Ler mais