Mostre que a função, apesar de contínua, não tem derivada em $x = 0$
Derivadas: Aleph 11 - Volume 2 Pág. 82 Ex. 20
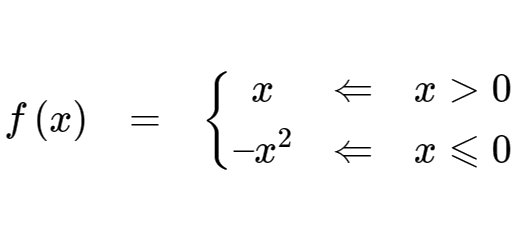
Mostre que a função $f$, de domínio $\mathbb{R}$, apesar de contínua, não tem derivada em $x = 0$:
\[\begin{array}{*{20}{c}}
{f\left( x \right)}& = &{\left\{ {\begin{array}{*{20}{c}}
x& \Leftarrow &{x > 0} \\
{ – {x^2}}& \Leftarrow &{x \leqslant 0}
\end{array}} \right.}
\end{array}\]
Resolução >> Resolução
<< Enunciado… Ler mais