Tagged: função afim
Qual é o número da rifa?
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 211 Tarefa 14
Lê o diálogo entre a Rita e o João.
Que número estava escrito na rifa comprada pela Rita? Explica a tua resposta.
Resolução >> Resolução
<< Enunciado… Ler maisCaminhando
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 210 Tarefa 13
A figura mostra as pegadas de um homem. O comprimento do passo, P, é a distância entre a parte de trás de duas pegadas consecutivas.
Para os homens, a fórmula estabelece uma relação aproximada entre n e P, em que
- n = número de passos por minuto, e
- P = comprimento do passo em metros.
- Se esta fórmula se aplicar ao caminhar do Pedro e ele der 70 passos por minuto, qual é o comprimento,
Caixas com bolos tradicionais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 209 Ex. 5
Numa banca de um arraial, estão à venda caixas com bolos tradicionais. Existem caixas com três bolos e existem caixas com quatro bolos.
Sabe-se ainda que:
- as caixas vazias têm todas a mesma massa;
- os bolos têm, também, todos a mesma massa;
- uma caixa com quatro bolos tem uma massa de 310 gramas;
- duas caixas, cada uma com três bolos, têm uma massa total de 470 gramas;
Qual é a massa, em gramas, de cada caixa vazia?… Ler mais
Duas retas representadas num referencial cartesiano
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 209 Ex. 4
Na figura, estão representadas, num referencial cartesiano, as retas r e s.
Sabe-se que:
- a reta r é definida por \(y = 0,6x\);
- a reta s é definida por \(y = – 1,2x + 4,5\);
- o ponto A é o ponto de interseção da reta s com o eixo das abcissas;
- o ponto B é o ponto de interseção da reta s com o eixo das ordenadas;
- o ponto I é o ponto de interseção das
A solução de outro sistema de equações
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 208 Ex. 3
Considera o seguinte sistema de equações.
\[\left\{ {\begin{array}{*{20}{l}}{x + y = 3}\\{2y = \frac{{x + y}}{3}}\end{array}} \right.\]
Qual é o par ordenado (x, y) que é solução do sistema?
Mostra como chegaste à tua resposta.
Resolução >> Resolução
<< Enunciado… Ler maisA solução de um sistema de equações
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 208 Ex. 2
Considera o seguinte sistema de equações.
\[\left\{ {\begin{array}{*{20}{l}}{\frac{x}{2} + y = 2}\\{x + 3y = 5}\end{array}} \right.\]
Qual dos quatro pares ordenados (x, y) seguintes é a solução do sistema?
[A] \(\left( { – 1,2} \right)\) [B] \(\left( {1,2} \right)\) [C] \(\left( { – 2,1} \right)\) [D] \(\left( {2,1} \right)\)
Resolução >> Resolução
<< Enunciado… Ler maisGraus Celsius e graus Fahrenheit
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 208 Ex. 1
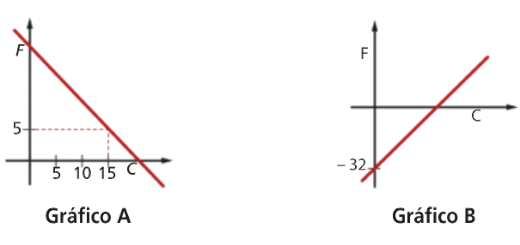
Para medir a temperatura podem utilizar-se termómetros graduados em graus Celsius ou termómetros graduados em graus Fahrenheit.
Para relacionar graus Celsius com graus Fahrenheit utiliza-se a fórmula \[F = 1,8C + 32\] em que C representa o valor da temperatura em graus Celsius e F representa o correspondente valor em graus Fahrenheit.
- Determina o valor da temperatura, em graus Fahrenheit, correspondente a −25 graus Celsius.
Mostra como chegaste à tua resposta. - Determina o valor da temperatura, em
Um retângulo com 28 cm de perímetro
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 207 Ex. 12
Um retângulo tem 28 cm de perímetro. O comprimento tem 2 cm a mais que a largura.
Quais são as dimensões desse retângulo?
[A] 3 cm e 5cm.
[B] 8 cm e 6 cm.
[C] 4 cm e 6 cm.
[D] 8 cm e 10 cm.
Resolução >> Resolução
<< Enunciado… Ler maisDois números
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 207 Ex. 11
A soma de dois números é 125. Um deles é igual a \(\frac{2}{3}\) do outro.
A diferença entre o maior e o menor, nessa ordem, é:
[A] 25 [B] 42 [C] 45 [D] 4
Resolução >> Resolução
<< Enunciado… Ler maisMais um sistema de equações
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 207 Ex. 10
A solução do sistema de equações \[\left\{ {\begin{array}{*{20}{l}}{2x – y = – 1}\\{y – 3x = – 1}\end{array}} \right.\] é o par ordenado \(\left( {x,y} \right)\).
O valor de \(xy\) é:
[A] −10 [B] 10 [C] 0 [D] 4
Resolução >> Resolução
<< Enunciado… Ler maisUm problema sobre os termos de uma fração
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 207 Ex. 9
Se \(\frac{x}{y}\) é uma fração equivalente a \(\frac{2}{7}\) e a soma dos seus termos é igual a 72, então \(x – y\) é igual a:
[A] −56 [B] 40 [C] −40 [D] 56
Resolução >> Resolução
<< Enunciado… Ler maisOs cromos da Joana e da Maria
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 207 Ex. 8
A Joana e a Maria têm, juntas, 360 cromos.
Se a Joana der 40 cromos à Maria, elas ficam com igual número de cromos.
O número de cromos da Joana é:
[A] 140 [B] 160 [C] 200 [D] 220
Resolução >> Resolução
<< Enunciado… Ler maisQual dos gráficos representa o sistema de equações?
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 207 Ex. 7
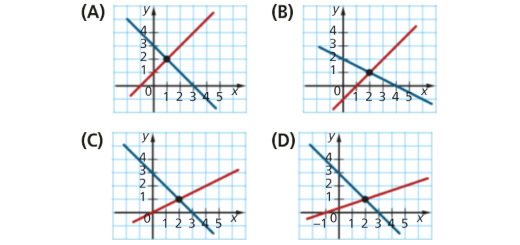
Indica qual dos gráficos abaixo representa o sistema seguinte.
\[\left\{ {\begin{array}{*{20}{l}}{x – 2y = 0}\\{x + y = 3}\end{array}} \right.\]
Resolução >> Resolução
<< Enunciado… Ler mais