Uma escultura em cimento
Derivadas: Aleph 11 - Volume 2 Pág. 89 Ex. 5
Enunciado
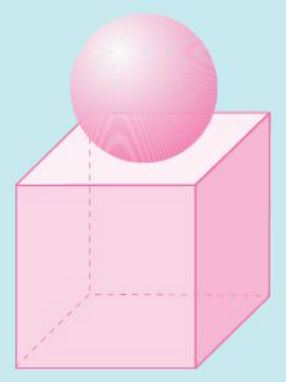Na figura, está representado um projeto de uma escultura em cimento para o jardim de uma escola, constituída por uma esfera colocada sobre um cubo.
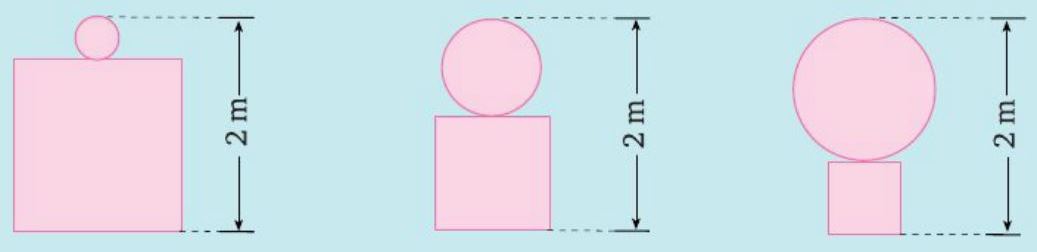
Pretende-se que a escultura tenha uma altura total de $2$ metros.
Apresentam-se, a seguir, as vistas de frente de três possíveis concretizações do projeto.
Designemos por $x$ o raio da esfera (em metros).
- Indique, na forma de intervalo de números reais, o conjunto dos valores que a variável $x$ pode assumir.
- Mostre que o volume total, em metros cúbicos, da escultura é dado, em função de $x$, por:
\[V\left( x \right) = \frac{{4\pi – 24}}{3}{x^3} + 24{x^2} – 24x + 8\] - Determine o raio da esfera e a aresta do cubo de modo que o volume total da escultura seja mínimo.
Apresente os resultados em metros, arredondados às centésimas.
Resolução
Como a escultura é constituída por uma esfera colocada sobre um cubo, com uma altura total de $2$ metros, resulta: $0 < 2x < 2 \Leftrightarrow 0 < x < 1$.
Logo, ${D_V} = \left] {0,1} \right[$.
- Para $x \in \left] {0,1} \right[$, vem:
\[\begin{array}{*{20}{l}}
{V\left( x \right)}& = &{{V_{Cubo}} + {V_{Esfera}}} \\
{}& = &{{{\left( {2 – 2x} \right)}^3} + \frac{4}{3}\pi {x^3}} \\
{}& = &{\left( {4 – 8x + 4{x^2}} \right)\left( {2 – 2x} \right) + \frac{4}{3}\pi {x^3}} \\
{}& = &{8 – 8x – 16x + 16{x^2} + 8{x^2} – 8{x^3} + \frac{4}{3}\pi {x^3}} \\
{}& = &{\frac{{4\pi – 24}}{3}{x^3} + 24{x^2} – 24x + 8}
\end{array}\]
- Para $x \in \left] {0,1} \right[$, vem:
\[\begin{array}{*{20}{l}}
{V’\left( x \right)}& = &{\frac{d}{{dx}}\left( {\frac{{4\pi – 24}}{3}{x^3} + 24{x^2} – 24x + 8} \right)} \\
{}& = &{3 \times \frac{{4\pi – 24}}{3}{x^2} + 48x – 24} \\
{}& = &{\left( {4\pi – 24} \right){x^2} + 48x – 24}
\end{array}\]
Determinemos os zeros de $V’$:
\[\begin{array}{*{20}{l}}
{V’\left( x \right) = 0}& \Leftrightarrow &{\begin{array}{*{20}{c}}
{x = \frac{{ – 48 \pm \sqrt {{{48}^2} + 96\left( {4\pi – 24} \right)} }}{{8\pi – 48}}}& \wedge &{x \in \left] {0,1} \right[}
\end{array}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{c}}
{x = \frac{{ – 48 \pm \sqrt {384\pi } }}{{8\pi – 48}}}& \wedge &{x \in \left] {0,1} \right[}
\end{array}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{c}}
{x = \frac{{ – 6 \pm \sqrt {6\pi } }}{{\pi – 6}}}& \wedge &{x \in \left] {0,1} \right[}
\end{array}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{c}}
{x = \frac{{6 \mp \sqrt {6\pi } }}{{6 – \pi }}}& \wedge &{x \in \left] {0,1} \right[}
\end{array}} \\
{}& \Leftrightarrow &{x = \frac{{6 – \sqrt {6\pi } }}{{6 – \pi }}}
\end{array}\]
Note que o único zero de $V’$ é:\[{x_1} = \frac{{6 – \sqrt {6\pi } }}{{6 – \pi }} \times \frac{{6 + \sqrt {6\pi } }}{{6 + \sqrt {6\pi } }} = \frac{{36 – 6\pi }}{{\left( {6 – \pi } \right)\left( {6 + \sqrt {6\pi } } \right)}} = \frac{{36 – 6\pi }}{{\left( {6 – \pi } \right)\left( {6 + \sqrt {6\pi } } \right)}} = \frac{6}{{6 + \sqrt {6\pi } }} = \frac{{\sqrt 6 \times \sqrt 6 }}{{\sqrt 6 \times \sqrt 6 + \sqrt 6 \times \sqrt \pi }} = \frac{{\sqrt 6 }}{{\sqrt 6 + \sqrt \pi }}\]
sendo \[V\left( {{x_1}} \right) = \frac{{8\pi }}{{{{\left( {\sqrt \pi + \sqrt 6 } \right)}^2}}}\]
O outro zero da equação do 2.º grau é:
\[{x_2} = \frac{{6 + \sqrt {6\pi } }}{{6 – \pi }} = \frac{{\sqrt 6 }}{{\sqrt 6 – \sqrt \pi }}\]
Construindo um quadro de sinal de $V’$, vem:$x$ $0$ $\frac{{\sqrt 6 }}{{\sqrt 6 + \sqrt \pi }}$ $1$ ${V’\left( x \right)}$ n.d. $ – $ $0$ $ + $ n.d. ${V\left( x \right)}$ n.d. $ \searrow $ $\frac{{8\pi }}{{{{\left( {\sqrt \pi + \sqrt 6 } \right)}^2}}}$ $ \nearrow $ n.d. Portanto, o volume total da escultura é mínimo para ${x_1} = \frac{{\sqrt 6 }}{{\sqrt 6 + \sqrt \pi }} \approx 0,58$ m (raio da esfera) e $a = 2 – 2 \times \frac{{\sqrt 6 }}{{\sqrt 6 + \sqrt \pi }} \approx 0,84$ m (aresta do cubo).
