Um percurso de comboio
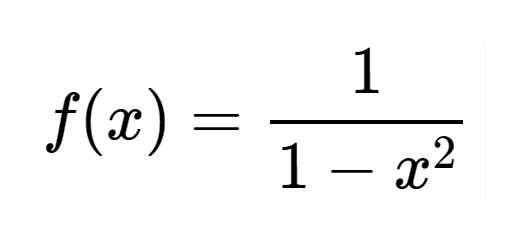
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 102 Ex. 6
Um comboio que anda à velocidade média de 75 km/h faz um certo percurso em 36 minutos.
Quanto tempo demoraria a fazer o mesmo percurso se andasse a uma velocidade média de 45 km/h?
Um comboio que anda à velocidade média de 75 km/h faz um certo percurso em 36 minutos.
Quanto tempo demoraria a fazer o mesmo percurso se andasse a uma velocidade média de 45 km/h?
Começando por tabelar os dados, temos:
| Comprimento do percurso (em km) | 45 | 45 |
| Velocidade média (em km/h) – \(v\) | 75 | 45 |
| Tempo gasto no percurso (em horas) – \(t\) | 0,6 | ? |
Ora, as grandezas \(v\) e \(t\) são inversamente proporcionais, pois o produto das correspondentes medidas é constante: \(v \times t = 45\).
Assim, vem:
\[\begin{array}{*{20}{l}}{45 \times t = 45}& \Leftrightarrow &{t = \frac{{45}}{{45}}}\\{}& \Leftrightarrow &{t = 1}\end{array}\]
Portanto, se o comboio andasse a uma velocidade média de 45 km/h, demoraria 1 hora a fazer o mesmo percurso.
Nota: \(36\;min = 36 \times \frac{1}{{60}}\;h = \frac{{6 \times 6}}{{6 \times 10}}\;h = 0,6\;h\).
