Pontos marcados num referencial
Isometrias: Matematicamente Falando 8 - Pág. 115 Ex. 5
Enunciado
Observa os pontos marcados no referencial da figura.
- Quais são as coordenadas do ponto D, imagem do ponto C pela translação de vetor \(\overrightarrow {BA} \)?
- Justifica que o quadrilátero [ABCD] é um paralelogramo.
- Determina o comprimento do segmento de reta [BC].
- O ponto E é a imagem do ponto A pela simetria central de centro C.
Indica as coordenadas de ponto E.
Resolução
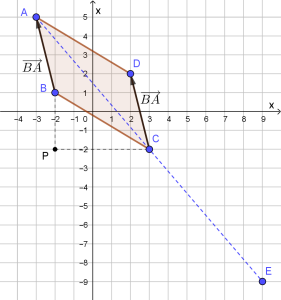Observa os pontos marcados no referencial da figura.
- O ponto D, imagem do ponto C pela translação de vetor \(\overrightarrow {BA} \), tem coordenadas \(\left( {2,2} \right)\).
- Os segmentos orientados [B, A] e [C, D] são equipolentes, bem como também são equipolentes os segmentos orientados [C, B] e [D, A]. Consequentemente, o quadrilátero [ABCD] possui os lados opostos paralelos, pelo que será, então, um paralelogramo.
- Aplicando o Teorema de Pitágoras no triângulo retângulo [BPC], temos: \(\overline {BC} = \sqrt {{{\overline {BP} }^2} + {{\overline {CP} }^2}} = \sqrt {{3^2} + {5^2}} = \sqrt {34} \).
- Como o ponto E é a imagem do ponto A pela simetria central de centro C, então C é o ponto médio do segmento de reta [AE]. As coordenadas de ponto E são \(\left( { – 9,9} \right)\).
