Cinco triângulos equiláteros iguais
Isometrias: Matematicamente Falando 8 - Pág. 115 Ex. 4
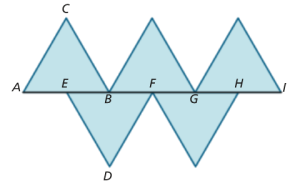
A figura abaixo é composta por triângulos equiláteros iguais.
Tem-se ainda que o ponto E é o ponto médio de [AB] e os pontos A, B, F, G, H e I estão alinhados.
- Existe uma reflexão deslizante que transforma o triângulo [ABC] no triângulo [DEF].
Identifica o eixo e o vetor associados a uma tal isometria. - Identifica uma reflexão deslizante que transforma o triângulo de lado [AB] no triângulo de lado [FH].
- Identifica o vetor que determina uma translação que transforma o triângulo de lado [AB] no triângulo de lado [GI].
- Identificas algum eixo de simetria nesta figura? Justifica.
A figura abaixo é composta por triângulos equiláteros iguais.
Tem-se ainda que o ponto E é o ponto médio de [AB] e os pontos A, B, F, G, H e I estão alinhados.
- Na reflexão deslizante que transforma o triângulo [ABC] no triângulo [DEF], o eixo de reflexão e o vetor associados a esta isometria são: AI e \(\overrightarrow {AE} \).
- Numa reflexão deslizante que transforma o triângulo de lado [AB] no triângulo de lado [FH], o eixo de reflexão e o vetor associados são: AI e \(\overrightarrow {AF} \).
- O vetor \(\overrightarrow {AG} \) determina uma translação que transforma o triângulo de lado [AB] no triângulo de lado [GI].
- Sim, identifico um eixo de simetria nesta figura: a reta perpendicular à reta AI e que contém o ponto F.