Daily Archive: Dezembro 8, 2022
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 66 Ex. 13
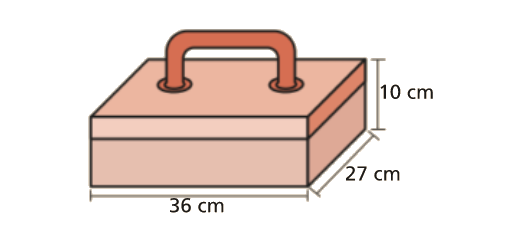
Enunciado
É possível colocar numa caixa de ferramentas, com 36 cm de comprimento, 27 cm de largura e 10 cm de altura, um pedaço de cano metálico de 42 cm de comprimento?
Explica a tua resposta.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 66 Ex. 12
Enunciado
A figura representa a vista lateral de uma rampa.
- Qual é a área da parte lateral da rampa?
- Calcula o comprimento da parte inclinada da rampa.
Resolução >>
Resolução
<< Enunciado…
Ler mais
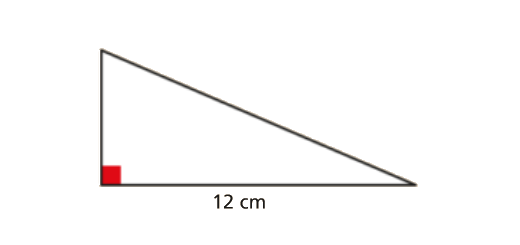
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 66 Ex. 11
Enunciado
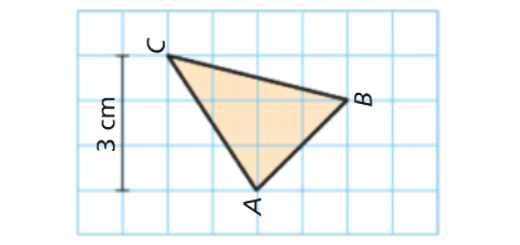
Considera o seguinte triângulo retângulo.
A área do triângulo é 54 cm2.
Determina o valor exato do seu perímetro.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 66 Ex. 10
Enunciado
Observa o papagaio de papel [ABCD].
\(\overline {AB} = 5,4\) cm; \(\overline {BC} = 8,5\) cm e \(\overline {BD} = 7,6\).
- Calcula o perímetro do papagaio.
- Qual é a área de papel gasto no papagaio?
(Sempre que necessário, usa valores aproximados às décimas.)
Resolução >>
Resolução
<< Enunciado…
Ler mais
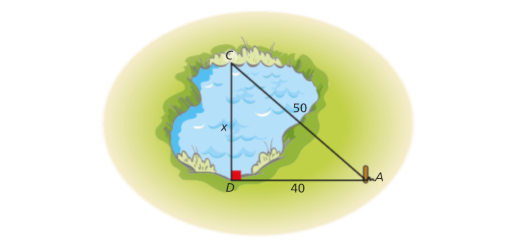
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 65 Ex. 9
Enunciado
Fixando uma estaca no ponto A e marcando os pontos C e D nas margens do lago, de modo que o ângulo ADC seja reto, a Catarina verificou que \(\overline {DA} = 40\) m e que \(\overline {AC} = 50\).
Qual é a distância entre os pontos C e D das margens do lago?
Resolução >>
Resolução
<< Enunciado…
Ler mais
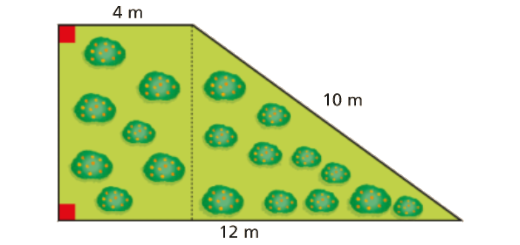
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 65 Ex. 8
Enunciado
A D.ª Rosalina possui o pomar representado na figura seguinte.
Determina a área do pomar da D.ª Rosalina.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 65 Ex. 7
Enunciado
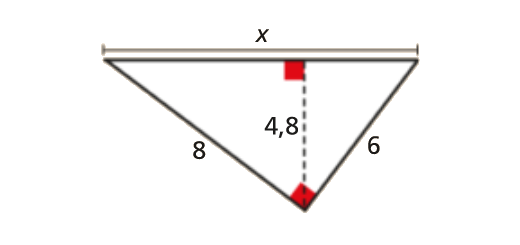
Determina o perímetro, arredondado às décimas, do triângulo [ABC].
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 65 Ex. 6
Enunciado
Um balão publicitário encontra-se preso ao solo por uma corda.
Num dia sem vento, estava suspenso na vertical, a 15 metros de altura. No entanto, no dia anterior esteve muito vento e o balão afastou-se 12 m do local onde se encontrava preso.
A que altura se encontrava?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 65 Ex. 5
Enunciado
Qual é a altura de um triângulo equilátero com 18 cm de perímetro?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 65 Ex. 4
Enunciado
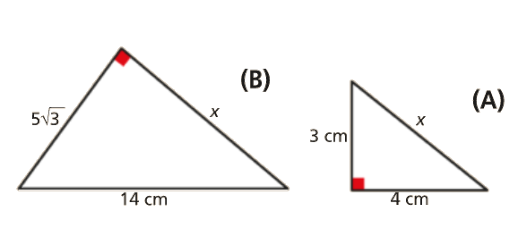
Aplicando o Teorema de Pitágoras, calcula o valor de x em cada caso.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 64 Ex. 3
Enunciado
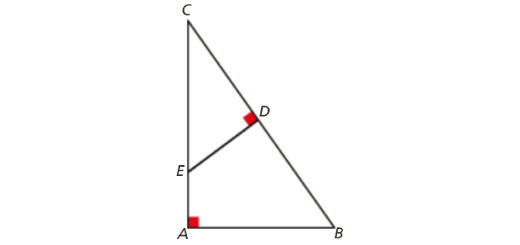
Na figura, estão representados dois triângulos, [ABC] e [EDC], retângulos, respetivamente em A e D, sendo E e D pontos, respetivamente, dos segmentos de reta [AC] e [BC].
- Justifica que os triângulos são semelhantes.
- Supondo que \(\overline {CB} = 10\) cm, \(\overline {CE} = 5\) cm e que \(\overline {DE} = 3\) cm, determina:
- a razão de semelhança que aplica o triângulo [CDE] no triângulo [CAB].
- a medida de \(\overline {CD} \).
- as medidas de \(\overline {AC}
…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 64 Ex. 2
Enunciado
Observa o escorrega, em que [AC] é perpendicular a [BC].
Qual é a altura do escorrega?
Resolução >>
Resolução
<< Enunciado…
Ler mais
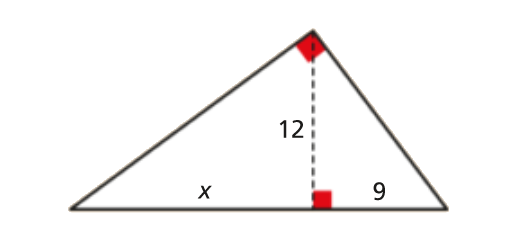
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 64 Ex. 1-C
Enunciado
Calcula o valor de x (unidade de comprimento: cm):
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 64 Ex. 1-B
Enunciado
Calcula o valor de x (unidade de comprimento: cm):
Resolução >>
Resolução
<< Enunciado…
Ler mais