A solução do sistema
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 202 Ex. 1
Encontra mentalmente a solução de cada um dos sistemas de equações.
Explica como fizeste.
\(\left\{ {\begin{array}{*{20}{l}}{x = \frac{1}{2}}\\{2x + y = 7}\end{array}} \right.\)
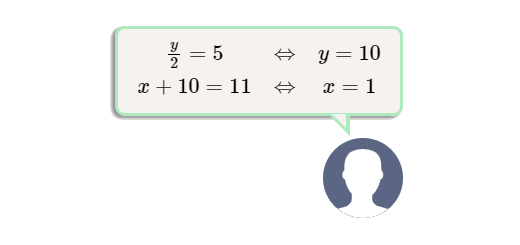
\(\left\{ {\begin{array}{*{20}{l}}{x + y = 11}\\{\frac{y}{2} = 5}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{x – y = 1}\\{y – 2 = 0}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{y = x + 5}\\{y = 2x}\end{array}} \right.\)
Resolução >> Resolução
<< Enunciado… Ler mais