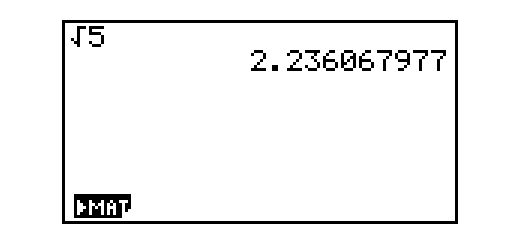Monthly Archive: Dezembro 2022
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 68 Ex. 5
Enunciado
A hipotenusa de um triângulo retângulo isósceles mede \(\sqrt {18} \) cm.
Os seus catetos podem medir:
[A] 3 cm; 3 cm.
[B] 9 cm; 9 cm.
[C] 3 cm; 9 cm.
[D] 4,24 cm; 4,24 cm.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 68 Ex. 4
Enunciado
Conhecem-se as medidas dos lados de quatro triângulos, I, II, III e IV.
| Triângulo |
Medida do lado \(a\) |
Medida do lado \(b\) |
Medida do lado \(c\) |
| I |
22 m |
17 m |
10 m |
| II |
37 m |
35 m |
12 m |
| III |
61 m |
60 m |
11 m |
| IV |
42 m |
31 m |
30 m |
Então, podemos dizer que são triângulos retângulos:
[A] Apenas os triângulos I e II.
[B] Apenas o triângulo III… Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 68 Ex. 3
Enunciado
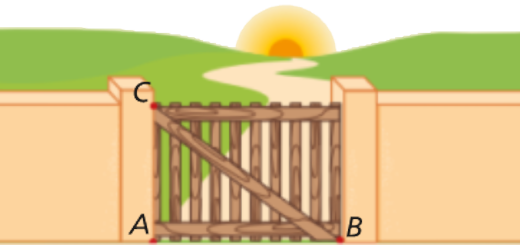
Na figura, vemos o portão de uma quinta com 2,3 m de comprimento e 0,9 metros de altura.
Qual é o comprimento, com aproximação ao decímetro, do reforço colocado na diagonal do portão?
[A] 2,1 m [B] 2,5 m [C] 2,0 m [D] 2,7 m
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 68 Ex. 2
Enunciado
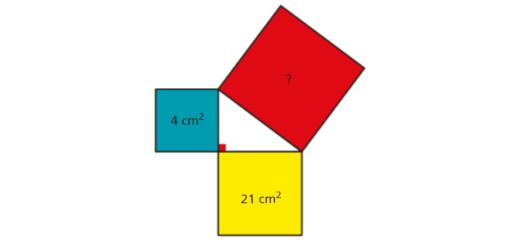
Sobre os lados do triângulo retângulo foram construídos três quadrados.
Qual é a área do quadrado vermelho?
[A] 37 cm2 [B] 17 cm2 [C] 29 cm2 [D] 25 cm2
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 68 Ex. 1
Enunciado
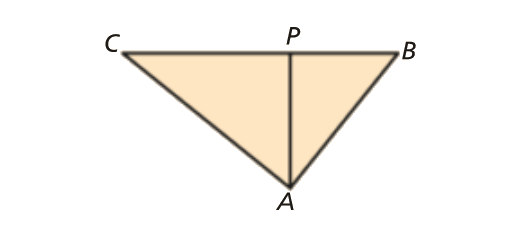
O triângulo [ABC] é retângulo em A, sendo [AP] a altura referente à hipotenusa.
Sabendo que \(\overline {AP} = 8\) cm e \(\overline {CP} = 10\) cm, qual é :
- o comprimento de [BP]?
[A] 6,4 cm [B] 10 cm [C] 7 cm [D] 8,2 cm
- o comprimento, aproximado às décimas, de cada um dos catetos de [ABC]?
[A] 6,4 cm e 19,3 cm.
[B] 10,2 cm e 12,8 cm.
[C] 10,2 cm e 19,3 cm.
[D]
…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 67 Ex. 20
Enunciado
Escreve, na forma de fração, em que o numerador e o denominador sejam números naturais, um número, x, que verifique a condição seguinte:
\[\sqrt 5 < x < 2,5\]
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 67 Ex. 19
Enunciado
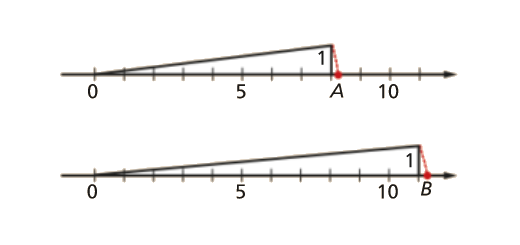
Indica os números irracionais representados pelos pontos A e B.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 67 Ex. 18
Enunciado
Considera os seguintes números reais:
| \(A \to \frac{7}{2}\) |
\(B \to – \frac{8}{3}\) |
\(C \to \sqrt 5 \) |
| \(D \to – \sqrt 2 \) |
\(E \to \sqrt 2 + 2\) |
\(F \to \sqrt 5 – 2\) |
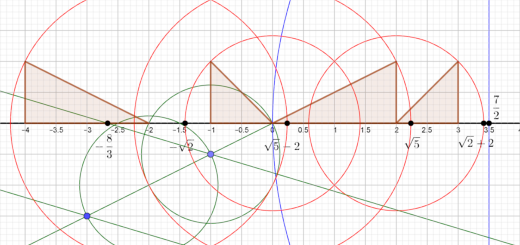
- Representa os números reais dados numa reta numérica.
- Escreve os números dados por ordem crescente.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 67 Ex. 16
Enunciado
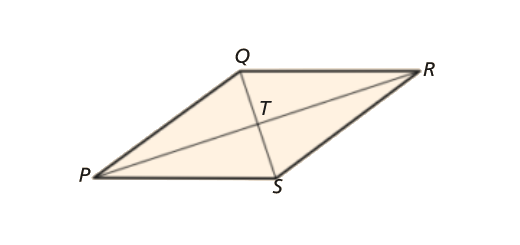
Considera um losango [PQRS], de perímetro 1 m, cujas diagonais se intersetam no ponto T.
Sabendo que [PT] tem 24 cm de comprimento, determina a área do losango.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 67 Ex. 15
Enunciado
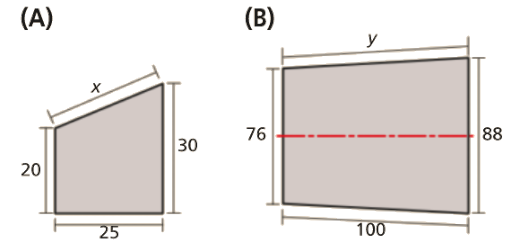
Observa as medidas, em milímetros, das bases de duas peças metálicas com a forma de trapézio.
O segmento de reta a vermelho é eixo de simetria de reflexão da figura (B).
- Determina x e y.
- Calcula o perímetro de cada uma das bases.
- Pretendendo forrar a papel as duas bases, quantos cm2 de papel se vão gastar em cada uma delas?
Apresenta o resultado arredondado às centésimas.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 66 Ex. 14
Enunciado
Quem chega a Lisboa, entrando pelo Tejo, encontra uma torre “torta”, mas elegante, que alberga o Centro de Coordenação e Controlo de Tráfego Marítimo.
A torre tem a forma de um prisma quadrangular oblíquo. A sua altura é de 36 m, e a torre está inclinada a sul, segundo um ângulo de cerca de 75°. Se o sol incidisse a pique sobre a torre, esta projetaria uma sombra retangular, em que um dos lados mediria, aproximadamente, … Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 66 Ex. 13
Enunciado
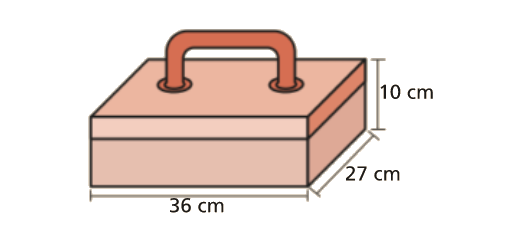
É possível colocar numa caixa de ferramentas, com 36 cm de comprimento, 27 cm de largura e 10 cm de altura, um pedaço de cano metálico de 42 cm de comprimento?
Explica a tua resposta.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 66 Ex. 12
Enunciado
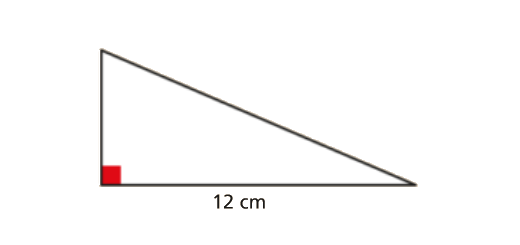
A figura representa a vista lateral de uma rampa.
- Qual é a área da parte lateral da rampa?
- Calcula o comprimento da parte inclinada da rampa.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 66 Ex. 11
Enunciado
Considera o seguinte triângulo retângulo.
A área do triângulo é 54 cm2.
Determina o valor exato do seu perímetro.
Resolução >>
Resolução
<< Enunciado…
Ler mais