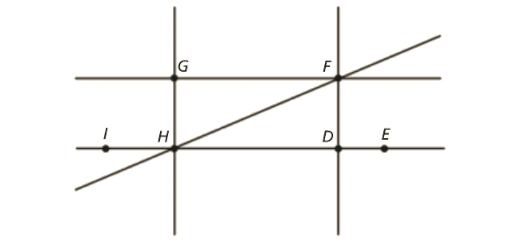
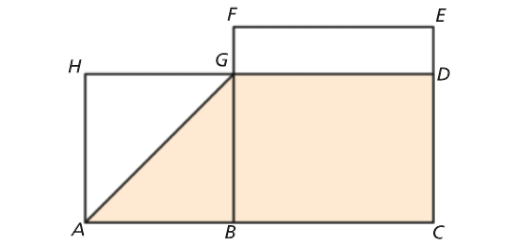
Observa outra figura
Isometrias: Matematicamente Falando 8 - Pág. 79 Tarefa 2
Indica, usando as letras da figura:
- dois segmentos de reta contidos na reta r;
- duas semirretas com a mesma origem;
- duas retas paralelas;
- duas retas perpendiculares;
- duas retas oblíquas;
- duas retas coincidentes;
- duas semirretas diretamente paralelas;
- duas semirretas inversamente paralelas.
Resolução >> Resolução
<< Enunciado… Ler mais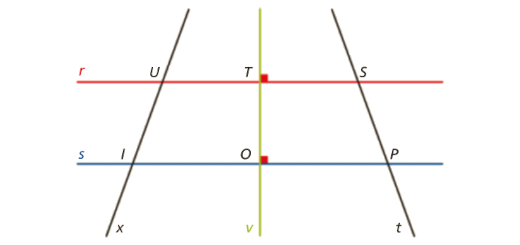















![Considera um triângulo retângulo [ABC]](https://www.acasinhadamatematica.pt/wp-content/uploads/2018/03/9V2Pag051-6-720x340.png)






