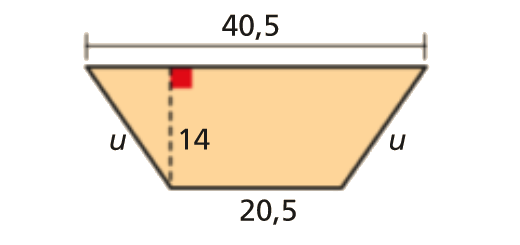
Um triângulo retângulo
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 61 Ex. 1
Considera um triângulo retângulo cuja hipotenusa mede \(\sqrt {10} \) cm.
- Indica dois números inteiros que sejam as medidas dos catetos.
- Marca na reta numérica o ponto correspondente a \(\sqrt {10} \).
Resolução >> Resolução
<< Enunciado… Ler mais