A Casinha da Matemática Blog
Isometrias: Matematicamente Falando 8 - Pág. 115 Ex. 5
Enunciado
Observa os pontos marcados no referencial da figura.
- Quais são as coordenadas do ponto D, imagem do ponto C pela translação de vetor \(\overrightarrow {BA} \)?
- Justifica que o quadrilátero [ABCD] é um paralelogramo.
- Determina o comprimento do segmento de reta [BC].
- O ponto E é a imagem do ponto A pela simetria central de centro C.
Indica as coordenadas de ponto E.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 115 Ex. 4
Enunciado
A figura abaixo é composta por triângulos equiláteros iguais.
Tem-se ainda que o ponto E é o ponto médio de [AB] e os pontos A, B, F, G, H e I estão alinhados.
- Existe uma reflexão deslizante que transforma o triângulo [ABC] no triângulo [DEF].
Identifica o eixo e o vetor associados a uma tal isometria.
- Identifica uma reflexão deslizante que transforma o triângulo de lado [AB] no triângulo de lado [FH].
- Identifica o vetor que determina
…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 115 Ex. 3
Enunciado
O triângulo [ABC] da figura desenhada pelo João é isósceles e retângulo em A.
- Qual é a amplitude do ângulo ABC? Porquê?
- Copia e constrói as imagens B’ de B e C’ de C pela translação que transforma A em A’.
- Sem utilizar a régua e o transferidor, indica, justificando:
a) os comprimentos dos segmentos de reta [A’C’] e [A’B’];
b) a amplitude do ângulo A’C’B’;
c) como classificas o triângulo [A’B’C’].
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 114 Ex. 2
Enunciado
O chão da cozinha da escola da Maria foi pavimentado com ladrilhos idênticos ao da figura da esquerda.
A figura da direita representa parte dessa pavimentação.
- Indica:
a) o transformado do ladrilho h pela reflexão de eixo AB;
b) o transformado do ladrilho h pela translação de vetor \(\overrightarrow {AB} \);
c) o transformado do ladrilho h pela rotação de centro C e amplitude 180°.
- Diz, justificando, se são verdadeiras ou falsas as seguintes afirmações:
a) A
…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 114 Ex. 1
Enunciado
Reproduz no teu caderno a figura seguinte e constrói a sua imagem por \({T_{\vec v}}\).
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 113 Ex. 7
Enunciado
A Ana imaginou o friso seguinte.
[A] O friso apresenta simetrias de translação e de rotação.
[B] O friso apresenta simetrias de reflexão axial e de rotação.
[C] O friso apresenta simetrias de translação e de reflexão deslizante.
[D] O friso apresenta simetrias de reflexão deslizante e de reflexão axial
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 113 Ex. 6
Enunciado
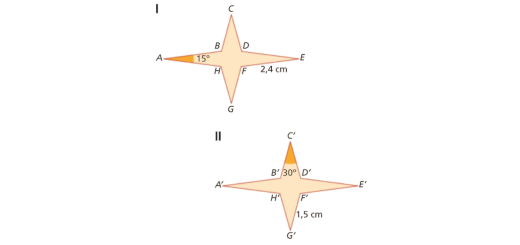
O polígono II foi obtido através de uma translação do polígono I.
Podemos afirmar que:
[A] O ângulo B’A’H’ mede 30°.
[B] O ângulo BCD mede 15°.
[C] O segmento de reta [FG] mede 1,5 cm.
[D] O segmento de reta [FG] mede 0,5 cm.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 113 Ex. 5
Enunciado
Observa as figuras.
As figuras F1 e F2 são imagens da figura F obtidas por meio das seguintes isometrias:
[A] Reflexão axial seguida de rotação;
[B] Reflexão deslizante seguida de rotação;
[C] Translação seguida de rotação;
[D] Rotação seguida de meia-volta.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 113 Ex. 4
Enunciado
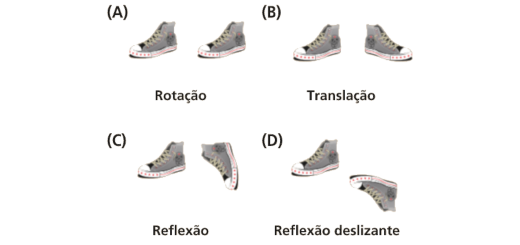
Em qual das situações, a isometria está bem identificada?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 112 Ex. 3
Enunciado
Considera os vetores \({\vec u}\) e \({\vec v}\) e as figuras que se seguem.
- Qual é o transformado da figura C por \({T_{\vec u}} \circ {T_{\vec v}}\)?
[A] A figura A.
[B] A figura B.
[C] A figura C.
[D] A figura D.
- Qual é o transformado da figura A pela translação de vetor \( – \vec u + \vec v\)?
[A] A figura A.
[B] A figura B.
[C] A figura C.
[D] A figura D.
…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 112 Ex. 2
Enunciado
Observa a figura.
A figura A é o transformado da figura B pela translação de vetor:
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 112 Ex. 1
Enunciado
Considera a figura que se segue.
- São um par de segmentos de reta orientados equipolentes:
(A) [A, B] e [B, A]
(B) [A, E] e [D, H]
(C) [G, H] e [G, I]
(D) [A, D] e [E, B]
- Identifica o vetor que não tem a mesma direção que os restantes.
(A) \(\overrightarrow {AC} \)
(B) \(\overrightarrow {EF} \)
(C) \(\overrightarrow {HG} \)
(D) \(\overrightarrow {CF} \)
- Dos seguintes vetores, qual é o que tem a mesma
…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 111 Ex. 22
Enunciado
Indica o tipo de simetria da figura, explicando o teu raciocínio.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 111 Ex. 21
Enunciado
O João desenhou as figuras usando papel quadriculado.
- Copia-as para o teu caderno e traça todos os eixo de simetria.
- Que simetrias de rotação observas em cada uma das figuras?
Resolução >>
Resolução
<< Enunciado…
Ler mais