A Casinha da Matemática Blog
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 177 Ex. 13
Enunciado
Observa os seguintes gráficos.
- Alguma das funções representadas é uma função linear?
Explica a tua resposta.
- Escreve a expressão algébrica da função f.
- O que têm de comum as duas retas?
- Qual é a ordenada na origem da reta que representa a função g?
- Determina uma expressão algébrica da função g.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 177 Ex. 12
Enunciado
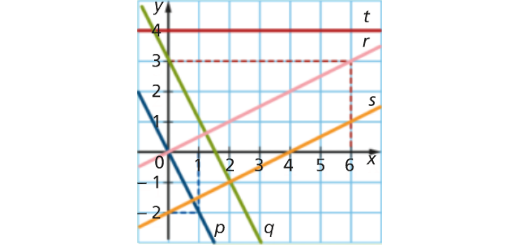
Na figura:
– as retas r e s são paralelas;
– as retas p e q são paralelas;
– a reta t é paralela ao eixo das abcissas.
Escreve as equações das cinco retas representadas na figura.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 176 Ex. 11
Enunciado
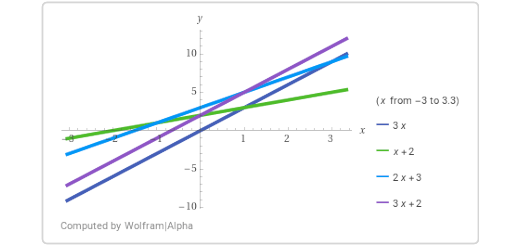
As equações das retas r, s, t e u são, respetivamente, \(y = 3x\), \(y = x + 2\), \(y = 2x + 3\) e \(y = 3x + 2\).
Quais as retas paralelas?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 176 Ex. 10
Enunciado
Considera os pontos \(A\left( {0, – 1} \right)\) e \(B\left( {1,0} \right)\).
- Assinala, nem referencial, os pontos A e B.
- Escreve uma equação da reta AB.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 176 Ex. 9
Enunciado
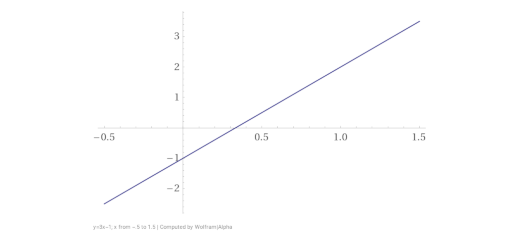
Quais são os valores do declive e da ordenada na origem da reta de equação \(y = 3x – 1\)?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 176 Ex. 8
Eunciado
Determina a expressão algébrica da função afim que corresponde a cada uma das seguintes representações gráficas.
Resolução >>
Resolução
<< Eunciado…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 176 Ex. 7
Enunciado
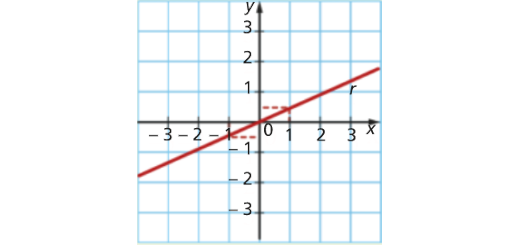
Escreve uma equação de cada uma das seguintes retas.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 176 Ex. 6
Enunciado
Escreve na forma canónica a expressão algébrica de cada uma das seguintes funções e indica se se trata de uma função constante, de uma função linear ou uma função afim.
| a) |
\(f\left( x \right) = 2 – 3x\) |
| b) |
\(g\left( x \right) = \frac{3}{2}\left( {x + 1} \right) + 5\) |
| c) |
\(h\left( x \right) = 5x – 3x\) |
| d) |
\(i\left( x \right) = 5 – \left( {x + 5} \right)\) |
| e) |
\(j\left( x \right) = 2\left( {x |
…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 175 Ex. 5
Enunciado
A potência de um motor pode ser entendida como a energia gerada por este, durante um determinado intervalo de tempo. São utilizadas várias unidades para medir a potência. Nos anúncios sobre automóveis a sua potência costuma ser indicada em cavalo (cavalo-vapor, cv).
No gráfico seguinte estabelece-se uma relação aproximada entre potência expressa em quilowatt (kW) e a potência expressa em cavalo-vapor.
- Justifica que a relação expressa no gráfico é de proporcionalidade direta.
- Transcreve a opção que corresponde
…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 175 Ex. 4
Enunciado
Sabe-se que as grandezas x e y são diretamente proporcionais.
| \(x\) |
\(2\) |
\( – \frac{1}{2}\) |
|
\(11\) |
|
| \(y\) |
\( – 8\) |
|
\( – 12\) |
|
\(20\) |
- Determina a constante de proporcionalidade.
- Copia e completa a tabela.
- Copia e completa a expressão: \(y = \ldots \times x\)
- Representa graficamente a função.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 175 Ex. 3
Enunciado
A turma da Marta desloca-se de Penafiel para Lisboa, num autocarro à velocidade média de 80 km/h. Considera para origem dos tempos e do espaço percorrido o instante em que fizeram uma paragem em Penafiel.
- Copia e completa a seguinte tabela.
| Tempo (horas) |
\( – 2\) |
\( – 1\) |
\(0\) |
\(1\) |
\(2\) |
| Espaço (km) |
\( – 160\) |
|
|
|
|
- O que significam os valores −2 horas e −160 km?
- Traduz esta situação por uma expressão algébrica e explica-a.
Resolução … Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 175 Ex. 2
Enunciado
Considera os pontos \(O\left( {0,0} \right)\) e \(A\left( {1,6} \right)\).
- Representa os pontos O e A num referencial cartesiano.
- Escreve uma equação da reta OA.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 175 Ex. 1
Enunciado
Os pontos M, N, O, P e Q estão representados no seguinte referencial cartesiano.
- Indica as coordenadas dos pontos N, O, P e Q.
- Assinala, num referencial cartesiano, os pontos: \(R\left( {1;0} \right)\), \(S\left( {0; – 1,5} \right)\) e \(T\left( { – 2,5; – \frac{1}{2}} \right)\).
- A que quadrante pertence o ponto de coordenadas \(\left( { – 1; – 3} \right)\)?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 174 Ex. 8
Enunciado
Determina as equações das seguintes retas.
Resolução >>
Resolução
<< Enunciado…
Ler mais