A Casinha da Matemática Blog
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 57 Ex. 5
Enunciado
Os números 3, 4 e 5 constituem o que se chama um terno pitagórico.
- Averigua se 6, 8 e 10 também formam um terno pitagórico.
- Escreve outro terno pitagórico.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 57 Ex. 4
Enunciado
Identifica quais dos seguintes triângulos são triângulos retângulos.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 57 Ex. 3
Enunciado
Existirá um triângulo retângulo em que os lados medem 3 cm, 5 cm e 7 cm?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 57 Ex. 2
Enunciado
Qual é o comprimento da diagonal de um retângulo com 4 cm de base e 6 cm de altura?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 57 Ex. 1
Enunciado
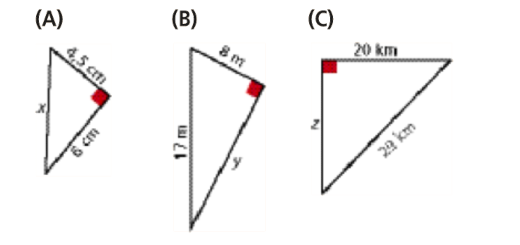
Calcula o valor do lado desconhecido em cada um dos seguintes retângulos.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 56 Tarefa 8 Ex. 2
Enunciado
O Pedro tem uma caixa cúbica.
A medida do comprimento da aresta da caixa é 6 cm.
Ajuda-o a saber qual é o comprimento máximo das palhinhas que cabem nessa caixa.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 56 Tarefa 8 Ex. 1
Enunciado
Observa a figura onde está representada uma caixa transparente, com a forma de um paralelepípedo retângulo, contendo uma caneta.
- Usando letras da figura, indica:
– Duas retas paralelas;
– Duas retas concorrentes não perpendiculares;
– Duas retas perpendiculares.
- Calcula, arredondado às décimas, o comprimento da sombra que a caneta projeta no fundo da caixa.
- A Marta pretende substituir a caneta por outra que mede 10 cm. Será que esta cabe na caixa?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 55 Tarefa 7
Enunciado
Na figura ao lado, está a fotografia de uma janela. No gradeamento exterior, podem observar-se diferentes polígonos, entre os quais vários retângulos e dois quadrados com o mesmo centro (os vértices do quadrado mais pequeno são os pontos médios das semidiagonais do quadrado maior).
Observa o seguinte esquema do gradeamento da janela.
Se o ferro para construir este tipo de gradeamento se vender em barras de 3 metros de comprimento, qual é o número mínimo de barras … Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 54 Tarefa 6
Enunciado
Num teste de Matemática, realizado pelo Vítor e pela Rita, apresentava-se a seguinte questão:
- O Vítor escolheu a opção A. Verifica se o Vítor respondeu corretamente. Apresenta todos os cálculos que efetuares.
- A Rita não conseguiu calcular a medida do comprimento da hipotenusa mas, mesmo assim, conseguiu eliminar cada uma das opções erradas. Indica uma razão que a Rita possa ter utilizado para eliminar a opção B e outra razão para eliminar a opção C.
…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 52 Tarefa 5
Enunciado
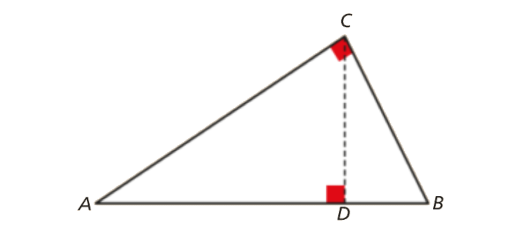
Considera o triângulo [ABC] retângulo em C , onde \(a = \overline {BC} \), \(b = \overline {AC} \) e \(c = \overline {AB} \).
Sejam [CD] a altura do triângulo relativa à hipotenusa, \(x = \overline {AD} \) e \(y = \overline {DB} \).
- Justifica que \({b^2} = xc\).
- Justifica que \({a^2} = yc\).
- Observando a figura e tendo em consideração as alíneas 1. e 2., mostra que \[{a^2} + {b^2} = {c^2}\]
Resolução >>
Resolução… Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 51 Tarefa 4
Enunciado
Observa as figuras compostas por triângulos retângulos e pelos quadrados construídos sobre a hipotenusa e sobre cada um dos catetos.
- Completa a tabela seguinte.
| Figura |
Área do quadrado assente sobre um dos catetos |
Área do quadrado assente sobre o outro cateto |
Área do quadrado assente sobre a hipotenusa |
| A |
|
|
|
| B |
|
|
|
| C |
|
|
|
- Qual é a relação entre as áreas dos quadrados de cada uma das figuras?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 50 Ex. 2
Enunciado
Um inseto parte do ponto M e percorre os segmentos [MA] e [AC], parando no ponto C.
Um outro inseto parte do ponto C e percorre os segmentos [CB] e [BM], parando no ponto M.
- Prova que os triângulos [AMC] e [CMB] são semelhantes.
- Determina:
– a distância que separa os dois insetos;
– a distância percorrida pelo primeiro inseto.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 48 Tarefa 3
Enunciado
O triângulo [ABC] é retângulo em C e [CD] é a altura do triângulo relativa à hipotenusa.
- Mostra que os triângulos [ABC] e [ACD] são semelhantes e que \[\frac{{\overline {AC} }}{{\overline {AB} }} = \frac{{\overline {AD} }}{{\overline {AC} }} = \frac{{\overline {CD} }}{{\overline {BC} }}\]
- Justifica que os triângulos [ABC] e [CDB] são semelhantes e que \[\frac{{\overline {BC} }}{{\overline {AB} }} = \frac{{\overline {BD} }}{{\overline {BC} }} = \frac{{\overline {CD} }}{{\overline {AC} }}\]
Resolução >>
Resolução
<< …
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 50 Ex. 1
Enunciado
Considera a figura, onde está representado um triângulo, retângulo em T e decomposto pela altura referente à hipotenusa.
- Justifica que os triângulos [TRH] e [TIH] são semelhantes.
- Estabelece a igualdade entre os ângulos correspondentes dos triângulos [TRH] e [TIH].
- Escreve as relações entre os comprimentos dos lados correspondentes dos triângulos [TRH] e [TIH].
- Determina a altura do triângulo [TRI].
Resolução >>
Resolução
<< Enunciado…
Ler mais