Monthly Archive: Novembro 2022
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 52 Tarefa 5
Enunciado
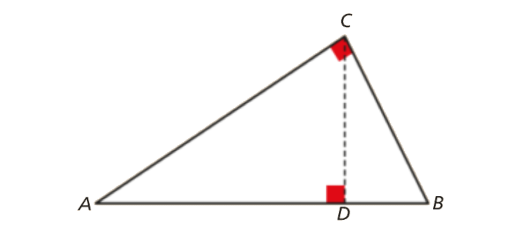
Considera o triângulo [ABC] retângulo em C , onde \(a = \overline {BC} \), \(b = \overline {AC} \) e \(c = \overline {AB} \).
Sejam [CD] a altura do triângulo relativa à hipotenusa, \(x = \overline {AD} \) e \(y = \overline {DB} \).
- Justifica que \({b^2} = xc\).
- Justifica que \({a^2} = yc\).
- Observando a figura e tendo em consideração as alíneas 1. e 2., mostra que \[{a^2} + {b^2} = {c^2}\]
Resolução >>
Resolução… Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 51 Tarefa 4
Enunciado
Observa as figuras compostas por triângulos retângulos e pelos quadrados construídos sobre a hipotenusa e sobre cada um dos catetos.
- Completa a tabela seguinte.
| Figura |
Área do quadrado assente sobre um dos catetos |
Área do quadrado assente sobre o outro cateto |
Área do quadrado assente sobre a hipotenusa |
| A |
|
|
|
| B |
|
|
|
| C |
|
|
|
- Qual é a relação entre as áreas dos quadrados de cada uma das figuras?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 50 Ex. 2
Enunciado
Um inseto parte do ponto M e percorre os segmentos [MA] e [AC], parando no ponto C.
Um outro inseto parte do ponto C e percorre os segmentos [CB] e [BM], parando no ponto M.
- Prova que os triângulos [AMC] e [CMB] são semelhantes.
- Determina:
– a distância que separa os dois insetos;
– a distância percorrida pelo primeiro inseto.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 48 Tarefa 3
Enunciado
O triângulo [ABC] é retângulo em C e [CD] é a altura do triângulo relativa à hipotenusa.
- Mostra que os triângulos [ABC] e [ACD] são semelhantes e que \[\frac{{\overline {AC} }}{{\overline {AB} }} = \frac{{\overline {AD} }}{{\overline {AC} }} = \frac{{\overline {CD} }}{{\overline {BC} }}\]
- Justifica que os triângulos [ABC] e [CDB] são semelhantes e que \[\frac{{\overline {BC} }}{{\overline {AB} }} = \frac{{\overline {BD} }}{{\overline {BC} }} = \frac{{\overline {CD} }}{{\overline {AC} }}\]
Resolução >>
Resolução
<< …
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 50 Ex. 1
Enunciado
Considera a figura, onde está representado um triângulo, retângulo em T e decomposto pela altura referente à hipotenusa.
- Justifica que os triângulos [TRH] e [TIH] são semelhantes.
- Estabelece a igualdade entre os ângulos correspondentes dos triângulos [TRH] e [TIH].
- Escreve as relações entre os comprimentos dos lados correspondentes dos triângulos [TRH] e [TIH].
- Determina a altura do triângulo [TRI].
Resolução >>
Resolução
<< Enunciado…
Ler mais
Exploração dinâmica da decomposição de um triângulo pela altura referente à hipotenusa, bem como a interpretação da relação de semelhança entre os triângulos obtidos.
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 47 Tarefa 2
Enunciado
Observa na figura o procedimento usado pela Marta para descobrir a distância entre as árvores que se encontram nos pontos A e B.
A medida do comprimento do seu passo é 80 cm.
- Justifica que os triângulos [ABC] e [ADE] são semelhantes.
- Qual é, em metros, a distância entre as árvores que se encontram nos pontos A e B?
Explica a tua resposta.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 47 Tarefa 1
Enunciado
A corda fixada nos pontos A e B e a corda fixada nos pontos C e D são paralelas.
Determina a distância que separa a Joana (ponto A) da árvore que está na outra margem do rio.
Explica a tua resposta.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Números reais: Matematicamente Falando 8 - Pág. 41 Ex. 10
Ununciado
Um retângulo tem de comprimento \(2\sqrt 3 + 2\) e de largura \(\sqrt 3 – 1\).
- Qual é a expressão simplificada que representa o perímetro do retângulo?
- Mostra que a área do retângulo é um número inteiro.
Resolução >>
Resolução
Um retângulo tem de comprimento \(2\sqrt 3 + 2\) e de largura \(\sqrt 3 – 1\).
-
Qual é a expressão simplificada que representa o perímetro do retângulo?
-
Mostra que a área do retângulo é um número inteiro.
…
Ler mais
Números reais: Matematicamente Falando 8 - Pág. 39 Ex. 16
Enunciado
Qual é o valor da expressão numérica \(2\sqrt 5 + 4\sqrt 5 – 5\sqrt 5 \)?
[A] \(\sqrt 5 \) [B] \(\sqrt {10} \) [C] \( – \sqrt 5 \) [D] \(5\)
Resolução >>
Resolução
<< Enunciado…
Ler mais
Números reais: Matematicamente Falando 8 - Pág. 37 Ex. 30
Enunciado
Associa a cada expressão o resultado correto:
| \(\sqrt 2 + \sqrt 2 \) |
A |
|
I |
\(2\) |
| \(\sqrt 2 \times \sqrt 2 \) |
B |
|
II |
\(\sqrt 2 \) |
| \(\frac{{10\sqrt 2 }}{5}\) |
C |
|
III |
\(2\sqrt 2 \) |
| \(\sqrt 2 \left( {\sqrt 2 – 1} \right)\left( {\sqrt 2 + 1} \right)\) |
D |
|
IV |
\(4\sqrt 2 \) |
| \(5\sqrt 2 – 3\sqrt 2 \) |
E |
|
|
|
| \({\left( {\sqrt 2 + 1} \right)^2} – {\left( {\sqrt 2 – 1} \right)^2}\) |
F |
|
|
|
| \({\left( {\frac{{\sqrt 2 |
…
Ler mais
Números reais: Matematicamente Falando 8 - Pág. 33 Ex. 6
Enunciado
Uma atleta treina de bicicleta ao redor de uma pista com forma e as dimensões abaixo.
- Qual é a distância, arredondada às unidades, percorrida pela atleta ao fim de uma volta completa?
- A roda da bicicleta da atleta tem 35 cm de raio.
Quantas voltas completas faz cada roda da bicicleta quando a atleta dá uma volta à pista?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Números reais: Matematicamente Falando 8 - Pág. 33 Ex. 5
Enunciado
Quais das seguintes afirmações são verdadeiras?
[A] O inverso de \( – 2\) é \(2\).
[B] O inverso de \(\sqrt {10} \) é \(\frac{1}{{\sqrt {10} }}\).
[C] O simétrico de \( – 2\) é \(2\).
[D] O simétrico de \(\sqrt {10} \) é \( – \frac{1}{{\sqrt {10} }}\).
Resolução >>
Resolução
<< Enunciado…
Ler mais
Números reais: Matematicamente Falando 8 - Pág. 33 Ex. 4
Ennciado
Calcula o valor exato de:
- \(\sqrt 3 \times \left( {1 + \frac{3}{{\sqrt 3 }}} \right)\)
- \({\left[ {{{\left( {\sqrt 5 } \right)}^2}} \right]^2}\)
- \(\frac{{7\pi – 3\pi }}{{2\pi }} \times \frac{{{{\left( {6\pi } \right)}^2}}}{{2\pi }}\)
Resolução >>
Resolução
<< Ennciado…
Ler mais