Dois insetos
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 50 Ex. 2
Enunciado
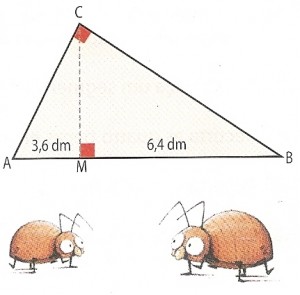Um inseto parte do ponto M e percorre os segmentos [MA] e [AC], parando no ponto C.
Um outro inseto parte do ponto C e percorre os segmentos [CB] e [BM], parando no ponto M.
- Prova que os triângulos [AMC] e [CMB] são semelhantes.
- Determina:
– a distância que separa os dois insetos;
– a distância percorrida pelo primeiro inseto.
Resolução
- Ambos os triângulos possuem um ângulo reto: ângulos AMC e BMC.
Os ângulos ACM e MCB são complementares, isto é, \(A\hat CM + M\hat CB = {90^{\rm{o}}}\).
Os ângulos ACM e MAC são também complementares, isto é, \(A\hat CM + M\hat AC = {90^{\rm{o}}}\). (Porquê?)
Logo, os ângulos MAC e MCB são geometricamente iguais.
Portanto, os triângulos [AMC] e [CMB] são semelhantes, pois possuem dois ângulos geometricamente iguais, cada um a cada um. - No final dos percursos, os insetos encontram-se, respetivamente, nos pontos C e M.
Logo, a distância que os separa é \(\overline {MC} \).
Como os triângulos considerados são semelhantes, então os comprimentos dos lados correspondentes são diretamente proporcionais. Isto é:
\[\frac{{\overline {AM} }}{{\overline {MC} }} = \frac{{\overline {MC} }}{{\overline {MB} }} = \frac{{\overline {AC} }}{{\overline {CB} }}\]
Logo, usando as duas primeiras razões, temos:
\[\begin{array}{*{20}{l}}{\frac{{3,6}}{{\overline {MC} }} = \frac{{\overline {MC} }}{{6,4}}}&{ \Leftrightarrow {\rm{\;}}}&{\overline {MC} \times \overline {MC} = 3,6 \times 6,4{\rm{\;}}}\\{}&{ \Leftrightarrow {\rm{\;}}}&{{{\overline {MC} }^2} = 23,04{\rm{\;}}}\\{}&{ \Leftrightarrow {\rm{\;}}}&{\overline {MC} = 4,8{\rm{\;}}}\end{array}\]
No final do percurso, os insetos encontram-se a 4,8 dm de distância.
A distância percorrida pelo primeiro inseto é \(\overline {MA} + \overline {AC} \).
Como os triângulos [ACM] e [ACB] (o menor e o maior dos triângulos) também são semelhantes, tem-se:
\[\frac{{\overline {AC} }}{{\overline {AB} }} = \frac{{\overline {MC} }}{{\overline {CB} }} = \frac{{\overline {AM} }}{{\overline {AC} }}\]
Logo, usando a primeira e terceira razões, temos:
\[\begin{array}{*{20}{l}}{\frac{{\overline {AC} }}{{10}} = \frac{{3,6}}{{\overline {AC} }}}&{ \Leftrightarrow {\rm{\;}}}&{{{\overline {AC} }^2} = 36{\rm{\;}}}\\{}&{ \Leftrightarrow {\rm{\;}}}&{\overline {AC} = 6{\rm{\;}}}\end{array}\]
Logo, a distância percorrida pelo primeiro inseto foi
\[\overline {MA} + \overline {AC} = 3,6 + 6 = 9,6{\mkern 1mu} dm\]
