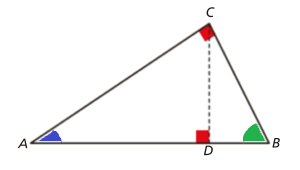
O triângulo [ABC] é retângulo
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 48 Tarefa 3
Enunciado
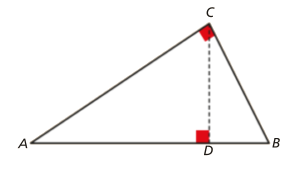O triângulo [ABC] é retângulo em C e [CD] é a altura do triângulo relativa à hipotenusa.
- Mostra que os triângulos [ABC] e [ACD] são semelhantes e que \[\frac{{\overline {AC} }}{{\overline {AB} }} = \frac{{\overline {AD} }}{{\overline {AC} }} = \frac{{\overline {CD} }}{{\overline {BC} }}\]
- Justifica que os triângulos [ABC] e [CDB] são semelhantes e que \[\frac{{\overline {BC} }}{{\overline {AB} }} = \frac{{\overline {BD} }}{{\overline {BC} }} = \frac{{\overline {CD} }}{{\overline {AC} }}\]
Resolução
O triângulo [ABC] é retângulo em C e [CD] é a altura do triângulo relativa à hipotenusa.
-
Mostra que os triângulos [ABC] e [ACD] são semelhantes e que \[\frac{{\overline {AC} }}{{\overline {AB} }} = \frac{{\overline {AD} }}{{\overline {AC} }} = \frac{{\overline {CD} }}{{\overline {BC} }}\]
-
Justifica que os triângulos [ABC] e [CDB] são semelhantes e que \[\frac{{\overline {BC} }}{{\overline {AB} }} = \frac{{\overline {BD} }}{{\overline {BC} }} = \frac{{\overline {CD} }}{{\overline {AC} }}\]
- O ângulo CAD é comum aos dois triângulos e os ângulos ACB e CDA, sendo ambos retos, são iguais.
Logo, pelo critério AA, os triângulos [ACD] e [ABC] são semelhantes.
Como os triângulos [ACD] e [ABC] são semelhantes, então os lados correspondentes têm comprimentos diretamente proporcionais (as razões estão escritas do triângulo menor para o maior):
\[\frac{{\overline {AC} }}{{\overline {AB} }} = \frac{{\overline {AD} }}{{\overline {AC} }} = \frac{{\overline {CD} }}{{\overline {BC} }}\] - O ângulo CBD é comum aos dois triângulos e os ângulos ACB e CDB, sendo ambos retos, são iguais.
Logo, pelo critério AA, os triângulos [CDB] e [ABC] são semelhantes.
Como os triângulos [CDB] e [ABC] são semelhantes, então os lados correspondentes têm comprimentos diretamente proporcionais (as razões estão escritas do triângulo menor para o maior):
\[\frac{{\overline {BC} }}{{\overline {AB} }} = \frac{{\overline {BD} }}{{\overline {BC} }} = \frac{{\overline {CD} }}{{\overline {AC} }}\]
Sobre os lados correspondentes de dois triângulos semelhantes
Em cada par de triângulos semelhantes, os lados correspondentes, em cada um dos dois triângulos, são os lados que se opõem, em cada triângulo, aos ângulos que são geometricamente iguais. E esta seleção de lados acontece três vezes, pois há três pares de lados que se opõem a três pares de ângulos geometricamente iguais.
Para evitar erros, quer para obter maior facilidade na identificação desses lados correspondentes, será recomendável destacar os três triângulos retângulos da figura original e colocá-los em linha, orientados segundo o cateto maior, por exemplo:
