A Casinha da Matemática Blog
Ainda os números: Matematicamente Falando 8 - Parte 1 Pág. 105 Ex. 1
Enunciado
Calcula as potências:
- ${{6}^{0}}$
- ${{(-5)}^{-1}}$
- ${{\left( \frac{1}{8} \right)}^{-1}}$
- ${{\left( \frac{7}{4} \right)}^{-1}}$
- ${{\left( -\frac{12}{5} \right)}^{-2}}$
- ${{\left( -\frac{6}{7} \right)}^{-3}}$
- ${{\left( \frac{3}{10} \right)}^{-4}}$
- ${{0,1}^{-1}}$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Ainda os números: Matematicamente Falando 8 - Parte 1 Pág. 99 Ex. 6
Enunciado
Determina o maior número de cestos que se pode encher com 180 maçãs e 252 laranjas, levando todos os cestos igual número de peças de fruta de cada qualidade.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Ainda os números: Matematicamente Falando 8 - Parte 1 Pág. 99 Ex. 5
Enunciado
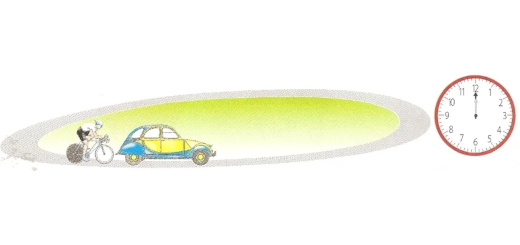
Um automobilista dá a volta a uma pista circular em 18 minutos e um ciclista em 32 minutos.
Se partirem ao meio-dia de um certo dia de um certo ponto da pista, a que horas se voltarão a encontrar? Nessa altura, quantas voltas terá dado cada um?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Ainda os números: Matematicamente Falando 8 - Parte 1 Pág. 99 Ex. 4
Enunciado
- Sabendo que o $m.d.c.(75,45)=15$, determina o m.m.c. entre os dois números.
- Sabendo que $m.m.c.(87,174)=174$, determina o m.d.c. entre os dois números.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Ainda os números: Matematicamente Falando 8 - Parte 1 Pág. 99 Ex. 3
Enunciado
Utilizando o m.m.c.,
- escreve por ordem crescente as fracções \[\begin{matrix}
\frac{7}{6}, & \frac{5}{9}, & \frac{19}{24} \\
\end{matrix}\]
- calcula \[\frac{5}{12}+\frac{4}{9}-\frac{3}{20}\]
Resolução >>
Resolução
<< Enunciado…
Ler mais
Ainda os números: Matematicamente Falando 8 - Parte 1 Pág. 99 Ex. 2
Enunciado
Utilizando a noção de m.d.c., torna irredutíveis as seguintes frações:
- $\frac{90}{75}$
- $\frac{297}{77}$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Ainda os números: Matematicamente Falando 8 - Parte 1 Pág. 89 Ex. 5
Enunciado
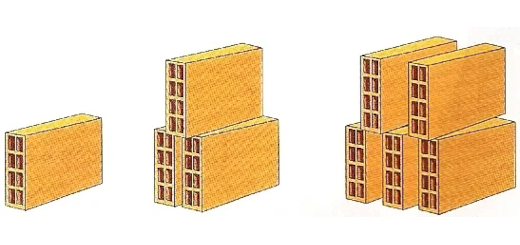
Considera a seguinte sequência formada por grupos de tijolos.
- Quantos tijolos devem ter os dois grupos seguintes?
- Escreve uma expressão geradora da sequência.
- Indica o número de tijolos do décimo grupo e do vigésimo segundo grupo.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Ainda os números: Matematicamente Falando 8 - Parte 1 Pág. 89 Ex. 4
Observa o seguinte triângulo formado por números.
\[\begin{matrix} \text{Linha 1} & {} & {} & {} & {} & 1 & {} & {} & {} & {} & {} \\ \text{Linha 2} & {} & {} & {} & 1 & 2 & 1 & {} & {} & {} & {} \\ \text{Linha 3} & {} & {} & 1 & 2 & 3 & 2 & 1 & {} & {} & {} \\ \text{Linha 4} & {} & 1 & 2 & 3 & 4 & 3 & 2 & 1 & {} & {} \\ \text{Linha 5} & 1 & 2 & 3 & 4 & 5 & 4 & 3 & 2 & 1 & {} \\ \end{matrix}\]
Na 3.ª linha deste triângulo numérico há 5 números e na 4.ª linha há 7 números.
Quantos números há na 112.ª linha?
Explica como chegaste à tua resposta.
Ler mais
Derivadas: Infinito 11 A - Parte 2 Pág. 194 Ex. 37
Enunciado
Do terraço de um prédio lançou-se uma bola para cima. A altura a (em decâmetros), a que a bola se encontra da rua, é dada em função do tempo (em segundos) pela expressão:
\[a(t)=-0,5{{t}^{2}}+4t+4,5\]
- Qual é a altura do terraço?
- Qual o intervalo de tempo em que a bola está acima dos 120 metros?
- Compare os valores da velocidade média nos intervalos [0, 2] e [2, 3]. Que conclui?
- Qual é a altura máxima que a bola
…
Ler mais
Derivadas: Infinito 11 A - Parte 2 Pág. 194 Ex. 36
Enunciado
A lei de Boyle afirma que, se a temperatura permanece constante, a pressão $p$ e o volume $v$ (em m3) de um certo gás dentro de um recipiente estão relacionados pela expressão
\[p=\frac{200}{v}\]
Determine a taxa de variação de $p$ em relação a $v$ para um volume:
- de $10\,{{m}^{3}}$;
- ${{v}_{0}}$ qualquer.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Derivadas: Infinito 11 A - Parte 2 Pág. 194 Ex. 35
Enunciado
Um balão esférico está a ser insuflado.
Determine a taxa de variação da área $S$ da superfície do balão em relação ao raio $r$:
- para $r=1$;
- para $r=5$.
Nota: A área da superfície esférica é dada por $A=4\pi {{r}^{2}}$.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Derivadas: Infinito 11 A - Parte 2 Pág. 193 Ex. 34
Enunciado
Um atleta percorre uma pista de 100 metros de modo a que a distância d(t), em metros, percorrida após t segundos, é dada por:
\[d(t)=0,2{{t}^{2}}+8t\]
Determine o valor da velocidade do atleta:
- no início da corrida;
- quando $t=10$ s;
- ao chegar à meta.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Derivadas: Infinito 11 A - Parte 2 Pág. 193 Ex. 33
Enunciado
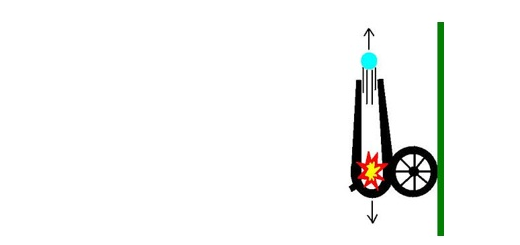
Um projétil é lançado do solo, verticalmente, com uma velocidade inicial de 115 m/s. Após $t$ segundos a sua distância $d$ ao solo é dada por:
\[d(t)=115t-5{{t}^{2}}\]
- Determine o valor da velocidade nos instantes $t=2$ e $t=3$.
- Quando é que o projétil atinge o solo?
Determine o valor da sua velocidade nesse instante.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Derivadas: Infinito 11 A - Parte 2 Pág. 193 Ex. 32
Enunciado
O perímetro $P$ de um círculo de raio $r$ é dado pela expressão $P=2\pi r$.
- Calcule a taxa média de variação de $P$ em cada um dos intervalos: $\left[ 2,9 \right]$, $\left[ 2;2,5 \right]$, $\left[ 2;2,1 \right]$, $\left[ 2;2,001 \right]$ e $\left[ 2,2+h \right]$.
- Qual é o valor da taxa de variação do perímetro para $r=2$?
Resolução >>
Resolução
<< Enunciado…
Ler mais