Um ângulo de vértice exterior a um círculo
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 135 Ex. 1
Enunciado
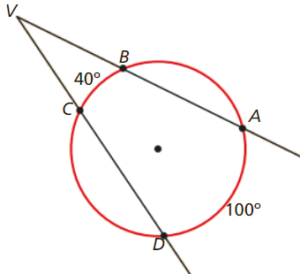Determina \(A\widehat VD\), sabendo que \(\overparen{AD} = 100^\circ \) e \(\overparen{BC} = 40^\circ \).
Resolução
Tendo em consideração que o ângulo AVD é um ângulo com vértice exterior a um círculo, vem:
\[A\widehat VD = \frac{{\overparen{AD} – \overparen{BC}}}{2} = \frac{{100^\circ – 40^\circ }}{2} = 30^\circ \]
ALTERNATIVA:
Tracemos a corda [AC] e reparemos que o ângulo ACD é um ângulo externo do triângulo [ACV].
Assim, temos:
\[A\widehat VD = A\widehat CD – C\widehat AV = \frac{{\overparen{AD}}}{2} – \frac{{\overparen{BC}}}{2} = \frac{{\overparen{AD} – \overparen{BC}}}{2} = \frac{{100^\circ – 40^\circ }}{2} = 30^\circ \]
Nota: A amplitude de um ângulo externo de um triângulo é igual à soma das amplitudes dos ângulos internos não adjacentes.
