A Casinha da Matemática Blog
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 29 Tarefa 6
Enunciado
Na figura está representada uma esfera de raio r e centro O.
A parte sombreada representa uma secção plana nela determinada por um plano perpendicular a [OP] e que contém os pontos B e C.
Os pontos A e B dividem o segmento [OP] em três partes iguais.
- Escreve, em função de r, o raio da secção plana sombreada.
- Sabendo que a área da secção é aproximadamente 20 cm2
…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 28 Ex. 6
Enunciado
Um cilindro reto com 40 cm de altura apresenta uma cavidade com a forma de um cone reto cuja base é concêntrica com a base do cilindro e com metade da altura deste.
Sabendo que o raio da base do cilindro mede 25 cm e que supera em 10 cm o raio da base do cone, calcula a área da superfície e o volume do sólido, arredondados às décimas.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 28 Ex. 5
Enunciado
Um sólido é formado por um cilindro e por dois cones retos com a mesma altura e cuja base é a base do cilindro.
O cilindro tem 18 cm de altura e 1152π cm3 de volume. A área da superfície do sólido é 560π cm2.
Qual é o volume do sólido?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 28 Ex. 4
Enunciado
Um cone reto com 28,5 cm de altura tem 13718π cm3 de volume.
Calcula:
- o valor exato da área da superfície do cone;
- a medida da amplitude do setor circular que se obtém quando se planifica o cone.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 28 Ex. 3
Enunciado
Um cone reto tem 1256 cm2 de área de superfície e a sua geratriz é tripla do raio da base.
Qual é a medida do comprimento, arredondado às unidades:
- o raio da base do cone?
- da geratriz do cone?
- da altura do cone?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 28 Ex. 1
Enunciado
Determina a área da superfície lateral de um cone com 10 cm de geratriz e 4 cm de raio da base.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 25 Ex. 6
Enunciado
Na figura está representado um prisma triangular.
Calcula:
- a área da sua superfície;
- o seu volume;
- o volume de uma pirâmide com a mesma base e a mesma altura do prisma.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 25 Ex. 4
Enunciado
A área da base de uma pirâmide quadrangular regular é igual a 25 cm2.
A altura de cada face lateral é 4 cm e a altura da pirâmide é, aproximadamente, 3,1 cm.
Determina:
- o volume da pirâmide;
- a área da superfície da pirâmide.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 25 Ex. 3
Enunciado
O perímetro da base de uma pirâmide triangular regular (pirâmide cuja base é um triângulo equilátero) é igual a 24 cm. A altura da face lateral da pirâmide é igual ao dobro da aresta da base e a altura da base mede aproximadamente 6,9 cm.
Determina:
- a área da superfície de uma das faces laterais;
- a área da base;
- a área da superfície da pirâmide.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 25 Ex. 2
Enunciado
Considera um prisma quadrangular regular cuja base tem 12 cm de perímetro e a medida da aresta lateral é a terça parte do perímetro da base.
- Calcula a área da sua superfície lateral.
- Determina o volume do prisma.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 22 Ex. 4
Enunciado
O diâmetro da Lua é aproximadamente um quarto do diâmetro da Terra.
Qual é a razão entre o volume da Lua e o da Terra?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 22 Ex. 3
Enunciado
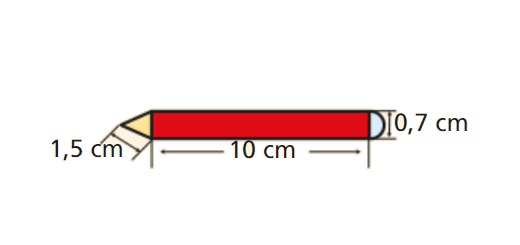
Calcula o volume do lápis representado a seguir.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 22 Ex. 2
Enunciado
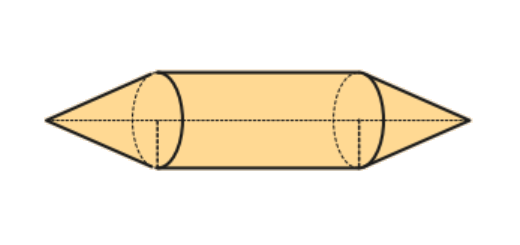
Observa as esculturas.
- Determina um valor arredondado às décimas do volume de cada uma delas.
- Qual é a quantidade de ferro gasta em cada uma das esculturas, sabendo que são maciças e que o ferro usado tem uma massa volúmica de 7,8 g/cm3.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 21 Ex. 7
Enunciado
Na figura está representado um sólido decomponível em dois cones com a mesma base (o círculo de diâmetro [AC]).
O quadrilátero [ABCD] é um losango de 72 cm2 de área, cuja diagonal menor ([AC]) mede metade da diagonal maior ([BD]).
- Determina a medida do comprimento das diagonais do losango.
- Calcula o volume do sólido.
Resolução >>
Resolução
<< Enunciado…
Ler mais























![O quadrilátero [ABCD] está dividido em dois triângulos retângulos](https://www.acasinhadamatematica.pt/wp-content/uploads/2018/03/9V2Pag056-9a-720x340.png)




