Um prisma triangular
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 25 Ex. 6
Enunciado
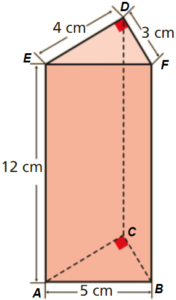Na figura está representado um prisma triangular.
Calcula:
- a área da sua superfície;
- o seu volume;
- o volume de uma pirâmide com a mesma base e a mesma altura do prisma.
Resolução
A área da superfície do prima é 156 cm2:
\[\begin{array}{*{20}{l}}{{A_T}}& = &{2 \times {A_{Base}} + {A_{Lateral}}}\\{}& = &{2 \times \frac{{\overline {BC} \times \overline {AC} }}{2} + \left( {\overline {AB} + \overline {BC} + \overline {CA} } \right) \times \overline {AE} }\\{}& = &{2 \times \frac{{3 \times 4}}{2} + \left( {5 + 3 + 4} \right) \times 12}\\{}& = &{156}\end{array}\]- O volume do prisma é 72 cm3:
\[\begin{array}{*{20}{l}}{{V_{Prisma}}}& = &{\frac{{\overline {BC} \times \overline {AC} }}{2} \times \overline {AE} }\\{}& = &{\frac{{3 \times 4}}{2} \times 12}\\{}& = &{72}\end{array}\] - O volume de uma pirâmide com a mesma base e a mesma altura do prisma é 24 cm3:
\[\begin{array}{*{20}{l}}{{V_{Pirâmide}}}& = &{\frac{1}{3} \times {V_{Prisma}}}\\{}& = &{\frac{1}{3} \times \frac{{\overline {BC} \times \overline {AC} }}{2} \times \overline {AE} }\\{}& = &{\frac{1}{3} \times \frac{{3 \times 4}}{2} \times 12}\\{}& = &{24}\end{array}\]
