O quadrilátero [ABCD] está dividido em dois triângulos retângulos
Trigonometria: Matematicamente Falando 9 - Parte 2 Pág. 56 Ex. 9
Enunciado
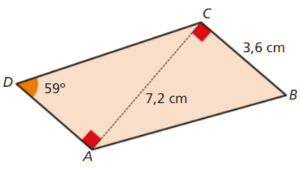O quadrilátero [ABCD] está dividido em dois triângulos retângulos.
- Qual é a medida da amplitude do ângulo BAC, arredondada às unidades? Explica como chegaste à tua resposta.
- Determina \(\overline {AD} \) arredondado às décimas.
Resolução
No triângulo retângulo [ABC], temos:
\[\begin{array}{*{20}{l}}{{\mathop{\rm tg}\nolimits} B\widehat AC = \frac{{\overline {BC} }}{{\overline {AC} }}}& \Leftrightarrow &{{\mathop{\rm tg}\nolimits} B\widehat AC = \frac{{3,6}}{{7,2}}}\\{}& \Leftrightarrow &{{\mathop{\rm tg}\nolimits} B\widehat AC = \frac{1}{2}}\\{}& \Leftrightarrow &{B\widehat AC = {{{\mathop{\rm tg}\nolimits} }^{ – 1}}\left( {\frac{1}{2}} \right)}\\{}&{}&{B\widehat AC \approx 27^\circ }\end{array}\]
Portanto, \({B\widehat AC \approx 27^\circ }\).
- No triângulo retângulo [ACD], temos:
\[\begin{array}{*{20}{l}}{{\mathop{\rm tg}\nolimits} A\widehat DC = \frac{{\overline {AC} }}{{\overline {AD} }}}& \Leftrightarrow &{{\mathop{\rm tg}\nolimits} 59^\circ = \frac{{7,2}}{{\overline {AD} }}}\\{}& \Leftrightarrow &{\overline {AD} = \frac{{7,2}}{{{\mathop{\rm tg}\nolimits} 59^\circ }}}\\{}&{}&{\overline {AD} \approx 4,3}\end{array}\]
Portanto, \({\overline {AD} \approx 4,3}\) cm.
