Um prisma quadrangular regular
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 25 Ex. 2
Enunciado
Considera um prisma quadrangular regular cuja base tem 12 cm de perímetro e a medida da aresta lateral é a terça parte do perímetro da base.
- Calcula a área da sua superfície lateral.
- Determina o volume do prisma.
Resolução
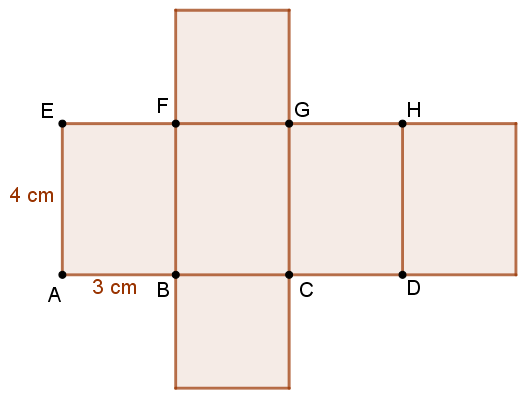
- Como o perímetro da base é 12 cm, então \(\overline {AB} = \overline {BC} = \overline {CD} = \overline {DA} = \frac{{12}}{4} = 3\) cm.
Como a medida da aresta lateral é a terça parte do perímetro da base, então \(\overline {AE} = \overline {BF} = \overline {CG} = \overline {DH} = \frac{{12}}{3} = 4\) cm.
Assim, a área da superfície lateral é \({A_L} = 4 \times \left( {\overline {AB} \times \overline {AE} } \right) = 4 \times \left( {3 \times 4} \right) = 48\) cm2.
- O prisma tem \(V = \left( {\overline {AB} \times \overline {BC} } \right) \times \overline {AE} = \left( {3 \times 3} \right) \times 4 = 36\) cm3 de volume.
