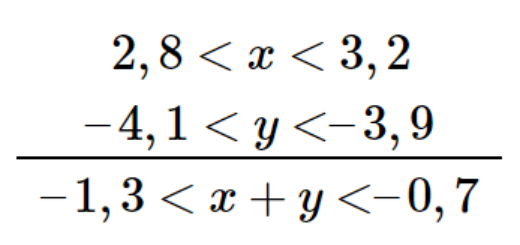A Álgebra é generosa; ela frequentemente dá mais do que aquilo que lhe é pedido. (D'Alembert)
Considera os seguintes enquadramentos de x e de y:
\[\begin{array}{*{20}{c}}{ – 2,3 < x < – 2,1}&{\rm{e}}&{ – 2,3 < x < – 2,1}\end{array}\]
Escreve o intervalo a que pertencem \(x + y\) e \(x \times y\).
Apresenta a tua resolução.
Resolução >> Resolução
<< Enunciado… Ler maisNa figura, está representado, num referencial ortogonal (eixos perpendiculares), um triângulo [ABC].
O segmento de reta [BC] é perpendicular ao eixo dos xx.
Um círculo tem 9,42 dm2 de área.
Determina valores aproximados a menos de uma centésima, um por defeito e outro por excesso, do perímetro desse círculo.
Resolução >> Resolução
<< Enunciado… Ler maisO trapézio retângulo da figura tem 39 cm2 de área.
Determina, com erro inferior a 0,1, dois valores aproximados, um por defeito e outro por excesso, da medida do perímetro do trapézio.
Resolução >> Resolução
<< Enunciado… Ler maisSabendo que um número \(x\) verifica a condição \(\frac{2}{3} < x < \frac{3}{4}\), enquadra os seguintes números:
Resolução >> Resolução
<< Enunciado… Ler maisObserva o retângulo [ABCD] da figura.
Resolução >> Resolução
<< Enunciado… Ler maisConsidera o triângulo da figura.
Indica os valores possíveis para o perímetro do triângulo.
Resolução >> Resolução
<< Enunciado… Ler maisUm terreno tem a forma de um triângulo isósceles [ABC], tal que \(\overline {AB} = \overline {AC} \) e P é um ponto do lado [AB] tal que \(\overline {PB} = 100\) m e \(\overline {AP} = \overline {BC} \).
Foram feitas duas medições aproximadas, respetivamente por defeito e por excesso, ao perímetro do terreno, tendo-se obtido os seguintes resultados: 821 metros e 827 metros.
Determina dois intervalos de amplitude inferior ou igual a 2, tais que … Ler mais
Pretende-se substituir painéis retangulares de dimensões 2,5 m e 3,5 m por painéis quadrados que tenham a mesma área.
Determina, com erro inferior a 1 dm e utilizando a tabela de quadrados perfeitos abaixo, dois valores aproximados, um por defeito e outro por excesso, da medida, em metros, do lado de cada um desses quadrados.
| \(x\) | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |
| \({x^2}\) | 676 | 729 | 784 | 841 | 900 | 961 | 1024 | 1089 | 1156 |
Enquadra \(\sqrt 7 \) por números racionais, com erro inferior a \(r = 0,5\).
Resolução >> Resolução
<< Enunciado… Ler maisSabe-se que \(2 < a < 3\) e que \(2 < b < 8\).
Aproxima por defeito às unidades \(\sqrt[3]{{a + 3b}}\).
Resolução >> Resolução
<< Enunciado… Ler maisEscreve um valor aproximado, por excesso, a menos de uma centésima, do número \(\sqrt 5 + \sqrt 7 \).
Resolução >> Resolução
<< Enunciado… Ler maisConsidera que \(3\) é uma aproximação de um número real \(x\) com um erro inferior a \(0,2\) e que \( – 4\) é uma aproximação de um número \(y\) com um erro inferior a \({0,1}\).
Qual é o erro máximo que se comete ao aproximar \(x + y\) por \(3 + \left( { – 4} \right) = – 1\)?
Resolução >> Resolução
<< Enunciado… Ler mais
Expresso
|
|
|
|
PÚBLICO Sítio com Matemática
