Indica os valores possíveis para o perímetro do triângulo
Os números reais: Matematicamente Falando 9 - Parte 1 Pág. 34 Ex. 4
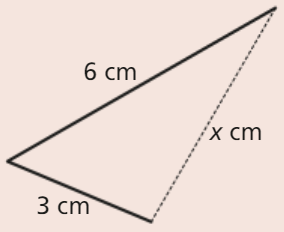 Considera o triângulo da figura.
Considera o triângulo da figura.
Indica os valores possíveis para o perímetro do triângulo.
Num triângulo, qualquer lado tem comprimento inferior à soma dos comprimentos dos outros dois lados.
Tendo em consideração a desigualdade triangular e que \({x > 0}\), vem:
\[\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{l}}{x > 0}\\{x < 3 + 6}\\{3 < x + 6}\\{6 < 3 + x}\end{array}} \right.}& \Leftrightarrow &{\left\{ {\begin{array}{*{20}{l}}{x > 0}\\{x < 9}\\{x > – 3}\\{x > 3}\end{array}} \right.}& \Leftrightarrow &{\left\{ {\begin{array}{*{20}{l}}{x > 3}\\{x < 9}\end{array}} \right.}& \Leftrightarrow &{3 < x < 9}\end{array}\]
Logo, \(\begin{array}{*{20}{c}}{3 < x < 9}& \Leftrightarrow &{3 + \left( {3 + 6} \right) < x + \left( {3 + 6} \right) < 9 + \left( {3 + 6} \right)}& \Leftrightarrow &{12 < x + \left( {3 + 6} \right) < 18}\end{array}\).
Assim, o perímetro do triângulo tem o seguinte enquadramento: \(12\;cm < P < 18\;cm\).















![Observa o triângulo [ABC], retângulo em A](https://www.acasinhadamatematica.pt/wp-content/uploads/2018/03/9V2Pag056-5a-720x340.png)


