Um trapézio retângulo
Os números reais: Matematicamente Falando 9 - Parte 1 Pág. 35 Ex. 11
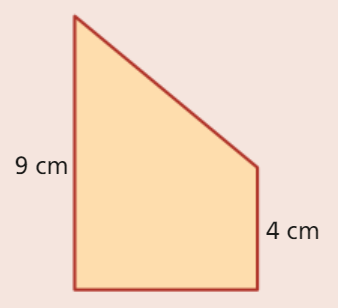 O trapézio retângulo da figura tem 39 cm2 de área.
O trapézio retângulo da figura tem 39 cm2 de área.
Determina, com erro inferior a 0,1, dois valores aproximados, um por defeito e outro por excesso, da medida do perímetro do trapézio.
 Comecemos por determinar a altura do trapézio, em centímetros:
Comecemos por determinar a altura do trapézio, em centímetros:
\[\begin{array}{*{20}{l}}{{A_{Trapézio}} = 39}& \Leftrightarrow &{\frac{{9 + 4}}{2} \times h = 39}\\{}& \Leftrightarrow &{h = 6}\end{array}\]
Determinemos agora o comprimento, em centímetros, do quarto lado do trapézio, utilizando o Teorema de Pitágoras:
\[x = \sqrt {{{\left( {9 – 4} \right)}^2} + {6^2}} = \sqrt {25 + 36} = \sqrt {61} \]
Enquadremos agora \(\sqrt {61} \) com erro inferior a \(0,1\):
\[\begin{array}{*{20}{c}}{{{78}^2} < {{10}^2} \times 61 < {{79}^2}}\\{{{\left( {\frac{{78}}{{10}}} \right)}^2} < 61 < {{\left( {\frac{{79}}{{10}}} \right)}^2}}\\{7,8 < \sqrt {52} < 7,9}\end{array}\]
Portanto, o perímetro do trapézio tem o seguinte enquadramento: \(26,8\;cm < {P_{Trapézio}} < 26,9\;cm\).













![O quadrilátero [ABCD] está dividido em dois triângulos retângulos](https://www.acasinhadamatematica.pt/wp-content/uploads/2018/03/9V2Pag056-9a-720x340.png)




