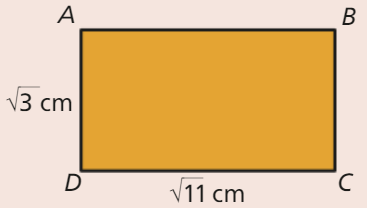
Observa o retângulo [ABCD] da figura
Os números reais: Matematicamente Falando 9 - Parte 1 Pág. 35 Ex. 5
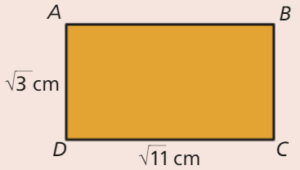Observa o retângulo [ABCD] da figura.
- Determina o valor exato do perímetro do retângulo [ABCD].
- Aproxima o valor da diagonal do retângulo [ABCD] às centésimas.
- Qual é o valor exato da área do retângulo [ABCD]?
Determina um intervalo de extremos racionais e de medida de comprimento inferior ou igual a \({\frac{1}{2}}\) e que contenha essa área.
O perímetro do retângulo da figura é \({P_{\left[ {ABCD} \right]}} = 2 \times \left( {\sqrt 3 + \sqrt {11} } \right)\) cm.- Aplicando o Teorema de Pitágoras no triângulo retângulo [ACD], temos: \(\overline {AC} = \sqrt {{{\overline {AD} }^2} + {{\overline {CD} }^2}} = \sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( {\sqrt {11} } \right)}^2}} = \sqrt {3 + 11} = \sqrt {14} \) cm.
Utilizando o método dos quadrados perfeitos, obtém-se o seguinte enquadramento:
\[\begin{array}{*{20}{c}}{{{374}^2} < {{100}^2} \times 14 < {{375}^2}}\\{{{\left( {\frac{{374}}{{100}}} \right)}^2} < 14 < {{\left( {\frac{{375}}{{100}}} \right)}^2}}\\{3,74 < \sqrt {14} < 3,75}\end{array}\]
Logo, \(3,74\;cm < \overline {AC} < 3,75\;cm\).
Como \(\left| {{{3,74}^2} – 14} \right| = 0,0124\) e \(\left| {{{3,75}^2} – 14} \right| = 0,0625\), então \(\overline {AC} \approx 3,74\;cm\), com aproximação às centésimas. - A área do retângulo [ABCD] é \({A_{\left[ {ABCD} \right]}} = \overline {AB} \times \overline {BC} = \sqrt {11} \times \sqrt 3 = \sqrt {33} \) cm2.
Utilizando novamente o método dos quadrados perfeitos, obtém-se o seguinte enquadramento:
\[\begin{array}{*{20}{c}}{121 < {2^2} \times 33 < 144}\\{{{11}^2} < {2^2} \times 33 < {{12}^2}}\\{{{\left( {\frac{{11}}{2}} \right)}^2} < 33 < {{\left( {\frac{{12}}{2}} \right)}^2}}\\{5,5 < \sqrt {33} < 6,0}\end{array}\]
Portanto, \({A_{\left[ {ABCD} \right]}} \in \left] {5,5;\;6,0} \right[\), em centímetros quadrados.
