Um terreno tem a forma de um triângulo isósceles
Os números reais: Matematicamente Falando 9 - Parte 1 Pág. 31 Ex. 8
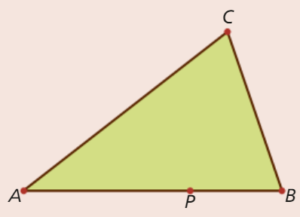Um terreno tem a forma de um triângulo isósceles [ABC], tal que \(\overline {AB} = \overline {AC} \) e P é um ponto do lado [AB] tal que \(\overline {PB} = 100\) m e \(\overline {AP} = \overline {BC} \).
Foram feitas duas medições aproximadas, respetivamente por defeito e por excesso, ao perímetro do terreno, tendo-se obtido os seguintes resultados: 821 metros e 827 metros.
Determina dois intervalos de amplitude inferior ou igual a 2, tais que a medida do comprimento, em metros, dos lados [AB] e [BC], pertençam respetivamente a esses intervalos.
De acordo com os dados, tem-se: \({P_{\left[ {ABC} \right]}} = 2 \times \overline {AB} + \overline {BC} = 2 \times \left( {\overline {BC} + 100} \right) + \overline {BC} = 3 \times \overline {BC} + 200\).
Assim, vem:
\[\begin{array}{*{20}{l}}{821 < {P_{\left[ {ABC} \right]}} < 827}& \Leftrightarrow &{821 < 3 \times \overline {BC} + 200 < 827}\\{}& \Leftrightarrow &{621 < 3 \times \overline {BC} < 627}\\{}& \Leftrightarrow &{207 < \overline {BC} < 209}\\{}& \Leftrightarrow &{\overline {BC} \in \left] {207,\;209} \right[}\end{array}\]
Por último, temos:
\[\begin{array}{*{20}{l}}{207 < \overline {BC} < 209}& \Leftrightarrow &{207 + 100 < \overline {BC} + 100 < 209 + 100}\\{}& \Leftrightarrow &{307 < \overline {AB} < 309}\\{}& \Leftrightarrow &{\overline {AB} \in \left] {307,\;309} \right[}\end{array}\]
