Graus Celsius e graus Fahrenheit
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 208 Ex. 1
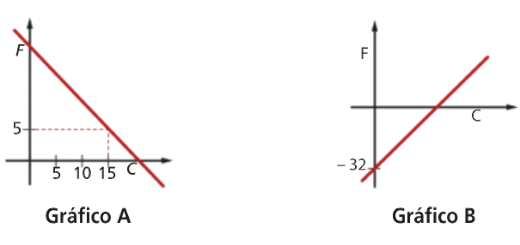
Para medir a temperatura podem utilizar-se termómetros graduados em graus Celsius ou termómetros graduados em graus Fahrenheit.
Para relacionar graus Celsius com graus Fahrenheit utiliza-se a fórmula \[F = 1,8C + 32\] em que C representa o valor da temperatura em graus Celsius e F representa o correspondente valor em graus Fahrenheit.
- Determina o valor da temperatura, em graus Fahrenheit, correspondente a −25 graus Celsius.
Mostra como chegaste à tua resposta. - Determina o valor da temperatura, em