A festa de final de ano
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 206 Ex. 4
A Associação de Estudantes da Escola Descobrir está a organizar a festa de final de ano, a realizar no ginásio. Vai ser uma festa em grande, já que o ginásio da escola tem capacidade para 400 alunos.
A Associação de Estudantes gastou 500 euros, na decoração e nos equipamentos de som e iluminação, e decidiu cobrar 2 euros por cada bilhete. O João e a Teresa estão encarregados de fazer a análise financeira da festa. Arranjaram uma expressão para calcular o saldo monetário da festa (S) em função do número de bilhetes vendidos (n): \[S = 2n – 500\]
- Qual é o lucro que a Associação pode esperar?
[A] 400 € [B] 800 € [C] 500 € [D] 300 € - No contexto da situação, a expressão \(2n\) significa:
[A] O lucro máximo que a Associação pode ter.
[B] O número de bilhetes comprados.
[C] O dinheiro obtido com a venda dos bilhetes.
[D] O prejuízo que a Associação pode ter. - Qual é o saldo monetário a apurar se forem vendidos 120 bilhetes?
[A] 260 € [B] −260 € [C] 740 € [D] −380 € - Quantos bilhetes, no mínimo, é necessário vender para que não haja prejuízo?
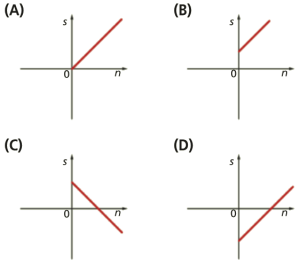
[A] 250 [B] 400 [C] 500 [D] 300 - Qual dos gráficos poderá representar a relação entre o saldo monetário, S, e o número de bilhetes vendidos, n?

A Associação de Estudantes da Escola Descobrir está a organizar a festa de final de ano, a realizar no ginásio. Vai ser uma festa em grande, já que o ginásio da escola tem capacidade para 400 alunos.
A Associação de Estudantes gastou 500 euros, na decoração e nos equipamentos de som e iluminação, e decidiu cobrar 2 euros por cada bilhete. O João e a Teresa estão encarregados de fazer a análise financeira da festa. Arranjaram uma expressão para calcular o saldo monetário da festa (S) em função do número de bilhetes vendidos (n): \[S = 2n – 500\]
- Qual é o lucro que a Associação pode esperar?
[A] 400 € [B] 800 € [C] 500 € [D] 300 €
Pode esperar um lucro máximo de 300 €, na suposição de esgotar a capacidade do ginásio da escola (venda de 400 bilhetes). - No contexto da situação, a expressão \(2n\) significa:
[A] O lucro máximo que a Associação pode ter.
[B] O número de bilhetes comprados.
[C] O dinheiro obtido com a venda dos bilhetes.
[D] O prejuízo que a Associação pode ter. - Qual é o saldo monetário a apurar se forem vendidos 120 bilhetes?
[A] 260 € [B] −260 € [C] 740 € [D] −380 €
Se forem vendidos 120 bilhetes, o saldo monetário a apurar é de \(S\left( {120} \right) = 2 \times 120 – 500 = – 260\) euros. - Quantos bilhetes, no mínimo, é necessário vender para que não haja prejuízo?
[A] 250 [B] 400 [C] 500 [D] 300
Para que não haja prejuízo, no mínimo, é necessário vender 250 bilhetes para que não haja prejuízo, pois \(\begin{array}{*{20}{c}}{S = 0}& \Leftrightarrow &{2n – 500 = 0}& \Leftrightarrow &{n = 250}\end{array}\) e a função S é crescente. - Qual dos gráficos poderá representar a relação entre o saldo monetário, S, e o número de bilhetes vendidos, n?
Pelas respostas anteriores, conclui-se que apenas a opção (D) satisfaz esses requisitos.
(Em alternativa, basta ter em consideração os valores do declive (2) e da ordenada na origem (−500) da reta que contém o gráfico da função S.)