Uma folha retangular de metal
Derivadas: Infinito 11 A - Parte 2 Pág. 198 Ex. 48
Uma folha retangular de metal com 20 cm de largura vai ser dobrada para se fabricarem caleiras, como mostra a figura.
Por onde devem ser feitas as dobragens para que a caleira transporte a maior quantidade possível de água?
Resolução >> Resolução
<< Resolução… Ler mais
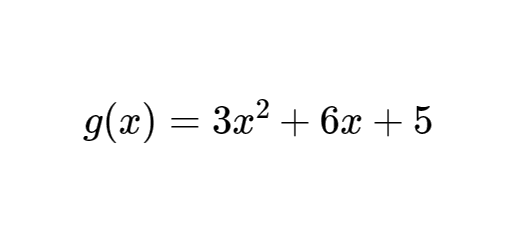





















![Uma corda [BC]](https://www.acasinhadamatematica.pt/wp-content/uploads/2018/03/9V2Pag60-2a-720x340.png)




