Uma corda [BC]
Trigonometria: Matematicamente Falando 9 - Parte 2 Pág. 60 Ex. 2
Enunciado
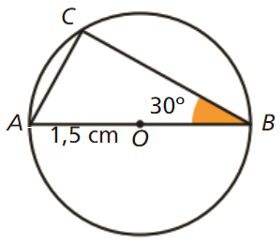Uma corda [BC] forma um ângulo de 30 graus com o diâmetro [AB] de uma circunferência, como vês na figura.
Qual é o comprimento da corda [AC], sabendo que o raio da circunferência mede 1,5 cm? Explica como chegaste à tua resposta.
Resolução
No triângulo retângulo [ABC] (Porquê?), temos \({\mathop{\rm sen}\nolimits} A\widehat BC = \frac{{\overline {AC} }}{{\overline {AB} }}\), donde:
\[\begin{array}{*{20}{l}}{{\mathop{\rm sen}\nolimits} 30^\circ = \frac{{\overline {AC} }}{{2 \times 1,5}}}& \Leftrightarrow &{\frac{1}{2} = \frac{{\overline {AC} }}{3}}\\{}& \Leftrightarrow &{\overline {AC} = \frac{3}{2}}\end{array}\]
Portanto, a corda [AC] tem 1,5 cm de comprimento.
