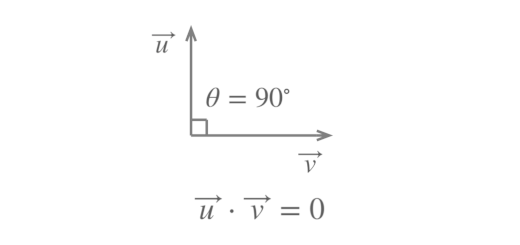A Casinha da Matemática

• Enunciado
• Resolução

Sendo $A(0,9)$ e $B(-8,2)$, identifique o conjunto de pontos $P(x,y)$ do plano que verificam a condição:

1. $\overrightarrow{AP}.\overrightarrow{BP}=0$;
2. $\overrightarrow{MP}.\overrightarrow{AM}=0$, sendo M o ponto médio de [AB].

Resolução >> Resolução

• Enunciado
• Resolução

Considere, num referencial o. n. $(O,\vec{i},\vec{j})$, a reta r de equação $(x,y)=(3,2)+k(-3,-1),k\in \mathbb{R}$ e o ponto $A(-1,4)$.

1. Determine a equação reduzida da reta s, perpendicular a r e que passa em A.
2. Desenhe um quadrado de vértice A, com um lado sobre a reta s e outro sobre a reta r, e determine, analiticamente, as coordenadas dos vértices do quadrado que construiu.

 Resolução >> Resolução

• Enunciado
• Resolução

Considere o triângulo [ABC], sendo $A(-5,1)$, $B(1,3)$ e $C(3,1)$.

1. Escreva uma equação cartesiana da mediatriz do lado [AB].
2. Escreva uma equação cartesiana da mediatriz do lado [BC].
3. Determine as coordenadas do ponto de intersecção das medianas determinadas (circuncentro ou centro da circunferência circunscrita no triângulo).
4. Escreva uma equação da circunferência circunscrita ao triângulo.

Resolução >> Resolução

• Enunciado
• Resolução

Num referencial o. n. $(O,\vec{i},\vec{j})$, considere a circunferência de equação ${{x}^{2}}+{{y}^{2}}+2x+4y+4=0$.

1. Determine as coordenadas do centro e o raio da circunferência.
2. Determine uma equação da reta tangente à circunferência no ponto $A(0,-2)$.

Resolução >> Resolução

• Enunciado
• Resolução

Considere um referencial o. n. $(O,\vec{i},\vec{j})$.

Escreva uma equação da circunferência circunscrita ao triângulo, cujos lados estão sobre as retas de equação $y=0$, $x=0$ e $y=x+4$.

Resolução >> Resolução

• Enunciado
• Resolução

1. Verifique que $A(1,-2)$ é o ponto da circunferência C: ${{x}^{2}}+{{y}^{2}}-6x-2y-3=0$ e escreva uma equação da reta tangente a C em A.
2. Determine uma equação da reta tangente à circunferência de centro $D(3,4)$ no ponto $E(1,2)$.

Resolução >> Resolução

• Enunciado
• Resolução

Sendo $A(2,1)$ e $B(-2,3)$, escreva uma equação da circunferência:

1. de centro A e que passa no ponto B;
2. de diâmetro [AB].

Resolução >> Resolução

• Enunciado
• Resolução

Considere os pontos $A(5,1)$, $B(-3,2)$ e $C(3,-2)$.

1. Escreva uma equação cartesiana da reta que contém a altura do triângulo [ABC] relativa a A.
2. Calcule a área do triângulo [ABC].

Resolução >> Resolução

• Enunciado
• Resolução

Averigue se são ou não perpendiculares as retas r e s de equações:

1. r: $y=2x-3$ e s: $y=-x+\frac{1}{2}$;
2. r: $x=3$ e s: $y=4$;
3. r: $2x+3y-1=0$ e s: $3x-2y+7=0$.

Resolução >> Resolução

• Enunciado
• Resolução

Seja $(O,\vec{i},\vec{j})$ um referencial o.n. do plano.

1. Escreva uma equação da reta que passa no ponto $A(2,3)$ e é perpendicular a $\vec{u}(-1,4)$ .
2. Escreva uma equação da reta que passa em $B(-3,4)$ e é perpendicular à recta de equação $2x-5y+1=0$.
3. Sejam $A(2,1)$ e $B(1,5)$ dois pontos do plano.
   Determine uma equação da mediatriz de [AB].

Resolução >> Resolução

• Enunciado
• Resolução

Seja $(O,\vec{i},\vec{j},\vec{k})$ um referencial o. n. do espaço.

1. Calcule a amplitude do ângulo formado pela diagonal de um cubo com qualquer das suas arestas.
2. O vetor ${\vec{u}}$  é tal que $\vec{u}=2\vec{i}+2\vec{j}+2\vec{k}$.
   Indique, em radianos, uma medida de $(\vec{u}\overset{\hat{\ }}{\mathop{{}}}\,\vec{i})$, de $(\vec{u}\overset{\hat{\ }}{\mathop{{}}}\,\vec{j})$ e de $(\vec{u}\overset{\hat{\ }}{\mathop{{}}}\,\vec{k})$.

Resolução >> Resolução

• Enunciado
• Resolução

Seja $(O,\vec{i},\vec{j})$ um referencial o. n. do plano.

Determine o ângulo que a reta r faz com a reta s:

1. r: $(x,y)=(1,3)+k.(-2,-2)\,,\,\,k\in \mathbb{R}$ e s: $3y-x-2=0$;
2. r: $x+2y+5=0$ e s: $y=\frac{3}{4}x-3$.

Resolução >> Resolução

• Enunciado
• Resolução

Averigue se o triângulo [ABC] é triângulo retângulo e isósceles, sendo:

1. $A(1,1,\sqrt{2})$, $B(\sqrt{2},-\sqrt{2},0)$ e C o simétrico de A em relação a O, origem do referencial;
2. $A(2,1,-3)$, $B(-1,3,4)$ e $C(-3,0,2)$.

Resolução >> Resolução

• Enunciado
• Resolução

Averigue se os vetores $\overrightarrow{u}$ e $\overrightarrow{v}$ são perpendiculares:

1. $\vec{u}(1,-3,2)$  e $\vec{v}(2,4,5)$
2. $\vec{u}(\sqrt{3}-1,4,-1)$  e $\vec{v}(\sqrt{3}+1,1,6)$
3. $\vec{u}(\frac{2}{3},-\frac{3}{2},\frac{5}{7})$  e $\vec{v}(-\frac{3}{2},\frac{2}{3},\frac{7}{5})$
4. $\vec{u}(-5,\alpha ,3)$  e  $\vec{v}(2\alpha ,10,0)$

Resolução >> Resolução