O monumento do Cristo Rei
Trigonometria: Matematicamente Falando 9 - Parte 2 Pág. 52 Ex. 10
O monumento do Cristo Rei foi inaugurado a 17 de maio de 1959.
É composto por um pedestal, com 82 m de altura, e pela estátua, com 28 m de altura.
- No momento em que o sol incide na estátua, fazendo com ela um ângulo de 50 graus, quanto mede o comprimento da sombra do monumento?
- Há momentos do dia em que a sombra de um objeto é igual à sua altura. Qual é a amplitude do



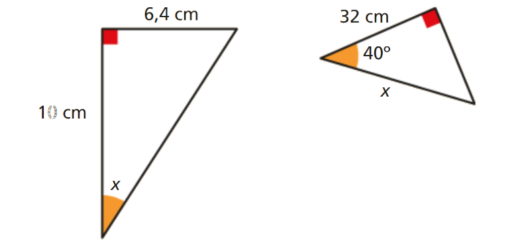
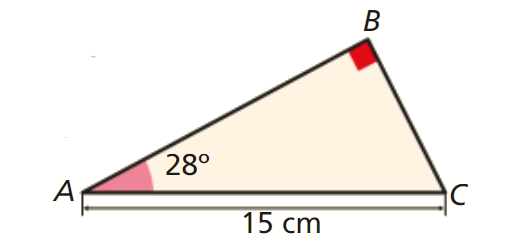

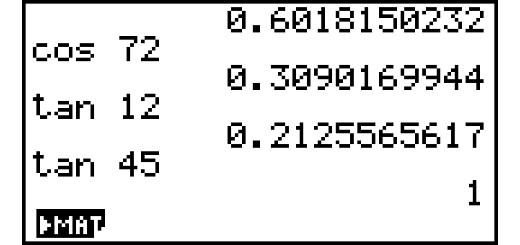















![Um triângulo [ABC]](https://www.acasinhadamatematica.pt/wp-content/uploads/2017/10/9V1Pag040-1_520x245.png)





