A Casinha da Matemática Blog
Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 39 Ex. 5
Enunciado
Um cone de revolução com 8 dm de altura tem por base um círculo com 6 dm de raio.
Quanto mede a sua geratriz?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 39 Ex. 4
Enunciado
Observa o prisma representado na figura:
- Indica, usando as letras da figura:
– duas retas paralelas;
– dois planos perpendiculares;
– uma reta e um plano perpendiculares;
– dois planos paralelos;
– uma reta paralela a um plano.
- Calcula o volume do prisma.
- Determina um valor aproximado às unidades da área total do prisma.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 39 Ex. 3
Enunciado
Cortou-se um cubo por um plano contendo as diagonais de duas faces paralelas.
- Que forma tem a secção obtida?
- Sabendo que o cubo tem 4 cm de aresta, relaciona a área da secção com a área de uma face.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 39 Ex. 2
Enunciado
O quarto do Fernando tem 2,45 m de altura.
Ele comprou um armário cujas medidas, em metros, estão indicadas na figura.
Ele conseguirá colocar o armário em pé sem ser preciso desmontá-lo?
Dica >>
Dica
<< Enunciado…
Ler mais
Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 39 Ex. 1
Enunciado
Qual o comprimento máximo que pode ter o varão de um cortinado que se deseja guardar provisoriamente numa arrecadação de 3 m de comprimento, 4 m de largura e 3 m de altura?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 191 Ex. 69
Enunciado
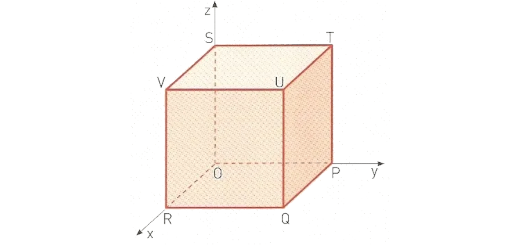
Na figura está representado um cubo, em referencial o.n. Oxyz.
Sabe-se que:
- a face [OPQR] está contida no plano xOy;
- a face [OSVR] está contida no plano xOz;
- a face [OSTP] está contida no plano yOz;
- uma equação do plano VTQ é $x+y+z=6$.
- Mostre que o volume do cubo é 27.
- Determine uma equação da superfície esférica, tal que:
– o centro é o simétrico de U, em relação ao plano xOy;
– o ponto Q pertence
…
Ler mais
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 191 Ex. 68
Enunciado
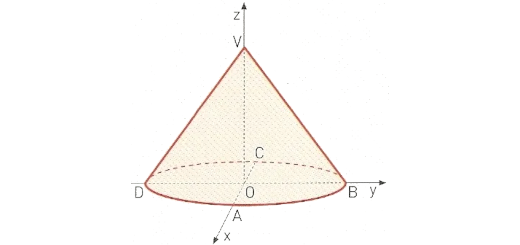
Na figura está representado, num referencial o.n. Oxyz, um cone de revolução.
Sabe-se que:
- A base do cone está contida no plano xOy e tem o seu centro na origem do referencial.
- [AC] e [BD] são diâmetros da base.
- O ponto A pertence ao semieixo positivo Ox.
- O ponto B pertence ao semieixo positivo Oy.
- O vértice V pertence ao semieixo positivo Oz.
- Sabendo que uma equação do plano ABV é $4x+4y+3z=12$, mostre que o comprimento do
…
Ler mais
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 190 Ex. 67
Enunciado
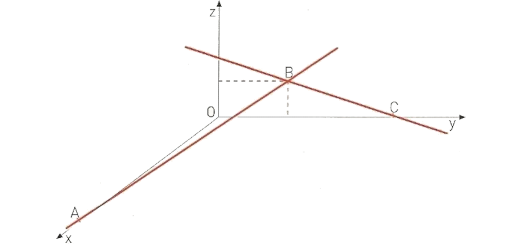
Considere num referencial ortonormado Oxyz:
- o ponto $A\,(10,0,0)$
- o ponto $B\,(0,2,1)$
- o ponto $C\,(0,5,0)$
- a recta AB
- a recta BC
- Justifique que as retas AB e BC são complanares e mostre que o plano $\alpha $ por elas definido admite como equação $x+2y+6z=10$.
- Determine uma equação vetorial da recta de intersecção do plano $\alpha $ com o plano xOz.
- Calcule o volume da pirâmide [OBCA].
Exercício extraído da Prova Modelo 1999 (questão 4 da 2.ª Parte)
EXAME … Ler mais
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 190 Ex. 66
Enunciado
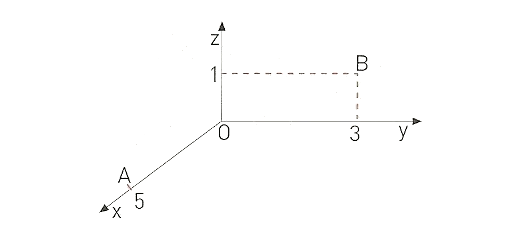
Considere, num referencial o.n. Oxyz, os pontos $A\,(5,0,0)$ e $B\,(0,3,1)$.
- Mostre que a reta AB está contida no plano de equação $x+2y-z=5$.
- Determine as coordenadas de um ponto C, pertencente ao eixo Oz e de cota positiva, de tal modo que o triângulo [ABC] seja retângulo em C.
- Determine o volume do cone que resulta da rotação do triângulo [AOB] em torno do eixo Ox.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 190 Ex. 65
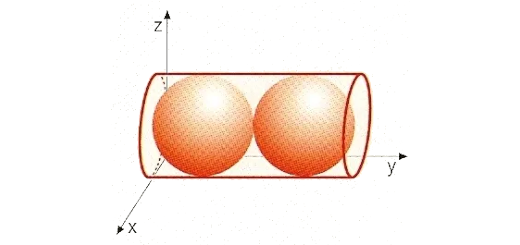
Enunciado
Na figura está representada, em referencial o.n. Oxyz, uma caixa cilíndrica construída num material de espessura desprezável.
A caixa contém duas bolas encostadas uma à outra e às bases da caixa cilíndrica.
- O cilindro tem uma das bases no plano xOz.
- O centro dessa base é o ponto de coordenadas $(3,0,3)$.
- A outra base está contida no plano de equação $y=12$.
- As bolas são esferas de raio igual a 3.
- Os diâmetros das esferas e das bases
…
Ler mais
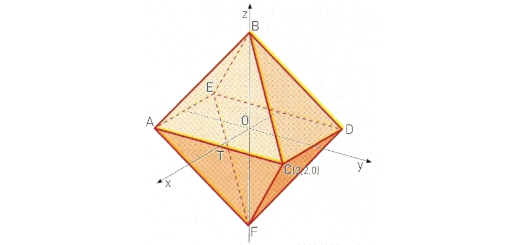
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 189 Ex. 64
Enunciado
Considere o referencial o.n. (O,x,y,z) e o octaedro regular representado na figura.
As arestas [AC], [CD], [DE] e [EA] estão contidas no plano xOy e o vértice B pertence ao eixo das cotas. O ponto C tem coordenadas $(2,2,0)$.
- Prove que o ponto B tem as coordenadas $(0,0,2\sqrt{2})$.
- Determine uma equação do plano ACB.
- Considere o plano de equação $x+y-2z=4$. Determine a sua intersecção com o plano xOy e mostre que o ponto C pertence a essa
…
Ler mais
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 189 Ex. 63
Enunciado
Suponha que a reta r: $x=y=z$ intersecta o plano $\alpha $: $x-2y-z=2$ no ponto P e o plano $\beta $: $x-2y-z=4$, no ponto Q.
Qual é, então, na unidade considerada, a norma do vector $PQ$?
Resolução >>
Resolução
<< Enunciado…
Ler mais
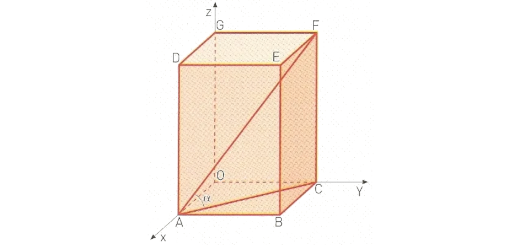
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 189 Ex. 62
Enunciado
A figura representa um paralelepípedo de altura variável, sendo:
- $\overline{AB}=4\,cm$
- $\overline{BC}=3\,cm$
- $\overrightarrow{AF}\overset{\hat{\ }}{\mathop{{}}}\,\overrightarrow{AC}=\alpha $
- Mostre que o volume do paralelepípedo é dado por $V(\alpha )=60\,tg\,\alpha $.
- Determine o valor exato do volume do sólido quando $\cos (\frac{\pi }{2}+\alpha )$ é igual a $-\frac{2}{3}$.
- Calcule o valor do produto escalar $\overrightarrow{AF}\,.\,\overrightarrow{BC}$.
- Se, no referencial o.n. representado, G for o ponto $(0,0,8)$, quais são as coordenadas dos pontos médios das arestas laterais do paralelepípedo?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 189 Ex. 61
Enunciado
Num referencial o.n. tridimensional, estão representados o ponto $A\,(2,-3,1)$ e o ponto $B\,(3,2,6)$.
- Determine a intersecção da reta AB com o plano xOy.
- Determine o lugar geométrico dos pontos equidistantes de A e de B.
Resolução >>
Resolução
<< Enunciado…
Ler mais