Triângulo inscrito na circunferência
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 129 Ex. 4
Enunciado
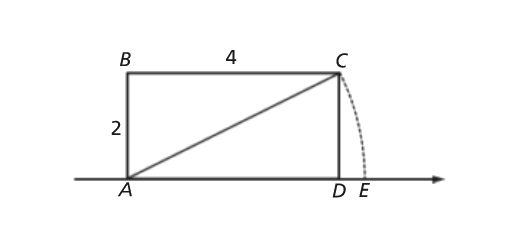
O triângulo [ABC] está inscrito na circunferência de centro O.
Determina a amplitude do comprimento do diâmetro [AC] da circunferência.
Resolução
O ângulo ABC é reto, pois está inscrito num arco de semicircunferência: \(A\widehat BC = \frac{{\overparen{AC}}}{2} = \frac{{180^\circ }}{2} = 90^\circ \).
Aplicando o Teorema de Pitágoras no triângulo retângulo [ABC], temos:
\[\overline {AC} = \sqrt {{{\overline {AB} }^2} + {{\overline {BC} }^2}} = \sqrt {{{12}^2} + {5^2}} = \sqrt {169} = 13\]
Portanto, \(\overline {AC} = 13\) cm.
