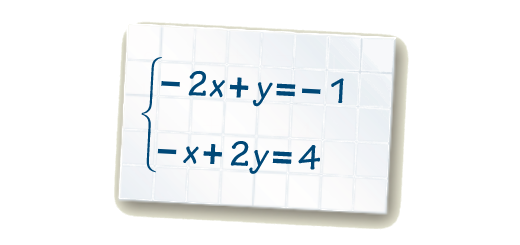A Casinha da Matemática Blog
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 202 Ex. 1
Enunciado
Encontra mentalmente a solução de cada um dos sistemas de equações.
Explica como fizeste.
\(\left\{ {\begin{array}{*{20}{l}}{x = \frac{1}{2}}\\{2x + y = 7}\end{array}} \right.\)
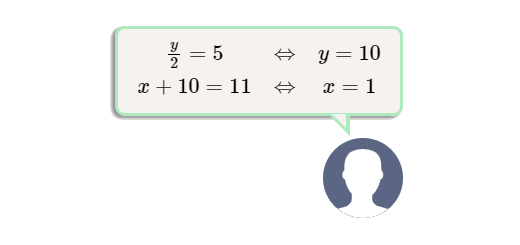
\(\left\{ {\begin{array}{*{20}{l}}{x + y = 11}\\{\frac{y}{2} = 5}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{x – y = 1}\\{y – 2 = 0}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{y = x + 5}\\{y = 2x}\end{array}} \right.\)
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 201 Tarefa 12
Enunciado
Considera os seguintes sistemas de equações:
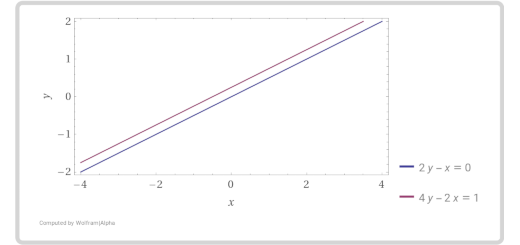
\[\begin{array}{*{20}{c}}{{\rm{(I)}}\left\{ {\begin{array}{*{20}{l}}{2y – x = 0}\\{4y – 2x = 1}\end{array}} \right.}&{{\rm{(II)}}\left\{ {\begin{array}{*{20}{l}}{x + y = – 4}\\{2x + 2y = – 8}\end{array}} \right.}&{{\rm{(III)}}\left\{ {\begin{array}{*{20}{l}}{x + y = 36}\\{3x – y = 44}\end{array}} \right.}\end{array}\]
- Resolve graficamente os sistemas (I), (II) e (III).
- Resolve cada um dos sistemas de equações, usando o método de substituição.
- Classifica os sistemas de equações.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 199 Tarefa 11
Enunciado
A Rita tem 5,50 euros no mealheiro. No total, tem 17 moedas, sendo umas de 20 cêntimos e outras de 50 cêntimos.
Seja x o número de moedas de 20 cêntimos e seja y o número de moedas de 50 cêntimos que a Rita tem no mealheiro.
- Indica qual dos sistemas seguintes permite determinar quantas moedas de 20 cêntimos e quantas moedas de 50 cêntimos tem a Rita no mealheiro.
\[\begin{array}{*{20}{l}}{{\rm{(A)}}\;\;\left\{ {\begin{array}{*{20}{l}}{x + y = 17}\\{\begin{array}{*{20}{l}}{20x +
…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 199 Tarefa 10
Enunciado
Considera o sistema de equações escrito no caderno da Joana.
- Resolve uma das equações em ordem a uma das incógnitas.
Escolhe bem a equação por onde queres começar de modo a facilitar os cálculos.
- Substitui, na outra equação, essa incógnita pela expressão obtida.
- Resolve a equação que ficou só com uma incógnita.
Que valor obtiveste?
- Substitui o valor encontrado na primeira equação.
- Escreve o par ordenado que é solução do sistema.
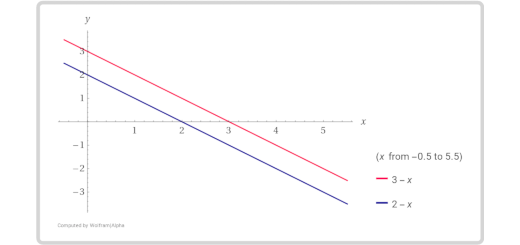
- Verifica graficamente se a solução obtida
…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 198 Tarefa 9
Enunciado
Observa as imagens e responde à questão colocada.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 197 Ex.6
Enunciado
Observa o seguinte sistema de equações.
\[\left\{ {\begin{array}{*{20}{l}}{x + 2y = 8}\\{\begin{array}{*{20}{l}}{2x + 4y = *}\end{array}}\end{array}} \right.\]
- Que número podemos colocar em * de modo a obtermos um sistema indeterminado?
- Sendo indeterminado, o sistema tem uma infinidade de soluções.
Apresenta quatro e representa-as num referencial cartesiano.
- Se a * for atribuído o número 10, qual é a posição relativa das retas que representam as equações?
Nesse caso, quantas soluções tem o sistema?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 197 Ex.5
Enunciado
Resolve graficamente os seguintes sistemas de equações e classifica-os, justificando.
\(\left\{ {\begin{array}{*{20}{l}}{x + y = 7}\\{\begin{array}{*{20}{l}}{x – y = 5}\end{array}}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{x = 3 – y}\\{\begin{array}{*{20}{l}}{2x + 2y = 4}\end{array}}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{x = 6 – y}\\{\begin{array}{*{20}{l}}{\frac{1}{2}x + \frac{1}{2}y = 3}\end{array}}\end{array}} \right.\)
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 197 Ex.4
Enunciado
Verifica, graficamente, se os sistemas são ou não equivalentes.
\[\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{l}}{x – y = 3}\\{\begin{array}{*{20}{l}}{2x + 2y = 10}\end{array}}\end{array}} \right.}&{\rm{e}}&{\left\{ {\begin{array}{*{20}{l}}{ – x + y = – 3}\\{\begin{array}{*{20}{l}}{x + y = 5}\end{array}}\end{array}} \right.}\end{array}\]
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 197 Ex.3
Enunciado
Considera o seguinte sistema de equações.
\[\left\{ {\begin{array}{*{20}{l}}{2x – y = 10}\\{x + y = 5}\end{array}} \right.\]
- Resolve cada uma das equações do sistema em ordem a y.
- Representa graficamente, no mesmo referencial, cada uma das equações do sistema.
- Classifica o sistema, indicando a sua solução.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 197 Ex.2
Enunciado
Escreve um sistema de equações para cada uma das situações.
| a) |
|
| b) |
|
| c) |
Um pai tem o quádruplo da idade do filho.
Daqui a 18 anos, a idade do pai será o dobro da idade do filho. |
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 197 Ex. 1
Enunciado
Averigua, em cada caso, se o par indicado é solução do sistema.
\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{2x + y = 10}\\{x – y = 2}\end{array}} \right.}&{}&{\left( {4,2} \right)}\end{array}\)
\(\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{l}}{2x + y = 12}\\{ – 3x + 4y = – 6}\end{array}} \right.}&{}&{\left( {5,2} \right)}\end{array}\)
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 196 Tarefa 8
Enunciado
Na bilheteira de um cinema, a Salomé viu um cartaz com duas opções para a compra de bilhetes.
Determina graficamente, em função do número x de sessões, a opção mais vantajosa para a Salomé.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 196 Tarefa 7
Enunciado
- Designando por x o dinheiro que a Salomé tem na carteira e por y o da Inês, traduz as afirmações através de duas equações.
- Representa, no mesmo referencial, as funções afins definidas por \(y = – \frac{1}{2}x + 10\) e \(y = 2x – 10\), e marca o ponto I que corresponde à sua interseção.
- Indica, a partir das representações gráficas anteriores, quais são as coordenadas do ponto I.
O que representam essas coordenadas?
- Há alguma
…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 190 Ex. 4
Enunciado
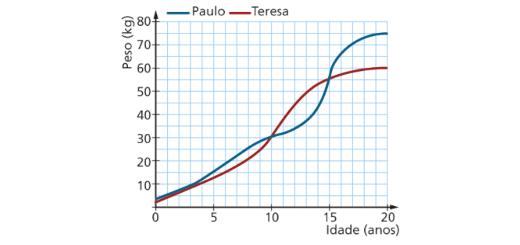
Os seguintes gráficos permitem comparar a evolução dos pesos do Paulo e da Teresa, ao longo dos seus anos de vida.
- Com que idades o Paulo e a Teresa pesavam o mesmo?
- Indica se a afirmação seguinte é verdadeira.
A Teresa, entre os 5 e os 10 anos, aumentou mais do que 10 kg e menos do que 15 kg.
- Para avaliar se uma pessoa é obesa, calcula-se o seu índice de massa corporal (IMC): \[IMC
…
Ler mais