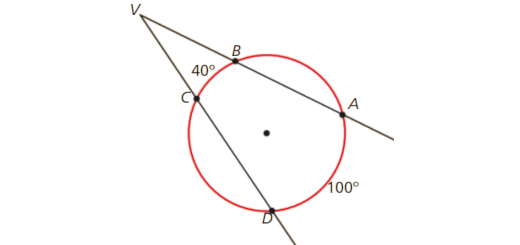
A Casinha da Matemática Blog
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 139 Ex. 4
Enunciado
A soma das amplitudes dos ângulos internos de um polígono convexo regular é 3780 graus.
Quantos lados tem esse polígono?
Explica como chegaste à tua resposta.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 139 Ex. 3
Enunciado
Calcula a soma das medidas das amplitudes dos ângulos internos de um:
- heptágono convexo.
- icoságono convexo.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 139 Ex. 2
Enunciado
Na figura, AEX é um ângulo externo de um pentágono [ABCDE] e \(\dot EY\) é a bissetriz desse ângulo.
- Qual é o valor de x?
- Qual é a medida da amplitude do ângulo externo AEX?
E a do ângulo interno AED?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 139 Ex. 1
Enunciado
Um polígono convexo tem 36 lados.
- Qual é a soma das amplitudes dos seus ângulos internos?
- Qual é a soma das amplitudes dos seus ângulos externos?
- Se o polígono for regular, qual é a amplitude de cada ângulo interno?
Resolução >>
Resolução
<< Enunciado…
Ler mais
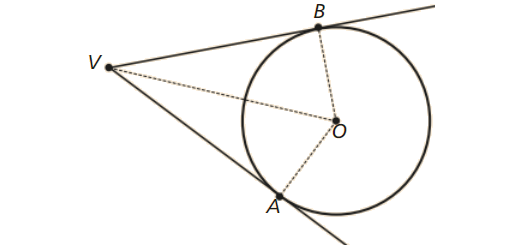
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 135 Ex. 7
Enunciado
Na figura, está representada uma circunferência de centro O e duas semirretas, concorrentes em V, e que são tangentes à circunferência nos pontos A e B.
- Justifica que \(\overline {VA} = \overline {VB} \).
- Supondo que a amplitude do arco AB mede 120 graus, determina a medida da amplitude do ângulo AVB.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 135 Ex. 6
Enunciado
Considera a circunferência de centro O e duas retas concorrentes CD e AB cujo ponto de interseção é E.
Sabe-se que \(\overparen{DB} = 3\overparen{AC}\) e \(\overparen{CB} = \overparen{AD} = 100^\circ \).
- Determina a amplitude dos arcos AC e DB.
- Qual é a amplitude de cada um dos ângulos internos do triângulo [ECB]?
Resolução >>
Resolução
<< Enunciado…
Ler mais
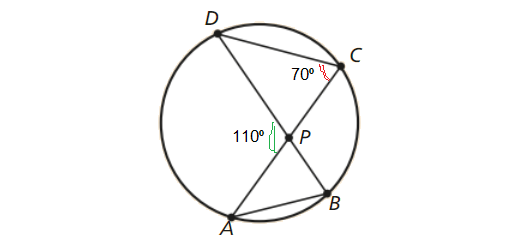
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 135 Ex. 5
Enunciado
Na figura, o ângulo ACD tem 70º de amplitude e o ângulo APD tem 110º de amplitude.
Determina a amplitude do ângulo BAC.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 135 Ex. 4
Enunciado
Observa a figura.
Determina o valor de cada uma das amplitudes p, q e r.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 135 Ex. 3
Enunciado
Na figura, a amplitude do arco AB é 100º e a do arco DF é 36º.
Calcula a amplitude do ângulo APB.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 135 Ex. 2
Enunciado
Observa as figuras seguintes e determina o valor de x.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 135 Ex. 1
Enunciado
Determina \(A\widehat VD\), sabendo que \(\overparen{AD} = 100^\circ \) e \(\overparen{BC} = 40^\circ \).
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 132 Ex. 5
Enunciado
Determina o valor de x em cada caso
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 132 Ex. 4
Enunciado
A semirreta \(\dot AX\) é tangente em A à circunferência de centro O e \(\alpha = 53^\circ \).
Calcula a medida das amplitudes dos ângulos AOB e BAX.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 132 Ex. 3
Enunciado
Observa a figura.
- Qual é a medida da amplitude x do ângulo de segmento assinalado na figura?
- Determina a medida da amplitude c do ângulo ao centro assinalado na figura.
Resolução >>
Resolução
<< Enunciado…
Ler mais