Um ângulo externo de um pentágono
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 139 Ex. 2
Enunciado
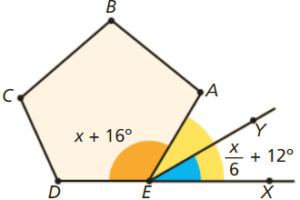Na figura, AEX é um ângulo externo de um pentágono [ABCDE] e \(\dot EY\) é a bissetriz desse ângulo.
- Qual é o valor de x?
- Qual é a medida da amplitude do ângulo externo AEX?
E a do ângulo interno AED?
Resolução
- Como \(\dot EY\) é a bissetriz do ângulo AEX, então \(A\widehat EY = Y\widehat EX\).
Dado que os ângulos DEA e AEX são adjacentes suplementares, vem:
\[\begin{array}{*{20}{l}}{x + 16^\circ + 2 \times \left( {\frac{x}{6} + 12^\circ } \right) = 180^\circ }& \Leftrightarrow &{3x + 48^\circ + x + 72^\circ = 540^\circ }\\{}& \Leftrightarrow &{4x = 420^\circ }\\{}& \Leftrightarrow &{x = 105^\circ }\end{array}\] 
\(A\widehat EX = 2 \times \left( {\frac{{105^\circ }}{6} + 12^\circ } \right) = 35^\circ + 24^\circ = 59^\circ \)
\(A\widehat ED = 105^\circ + 16^\circ = 121^\circ \)
