A Casinha da Matemática Blog
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 116 Ex. 9
Enumciado
A viagem aos Jogos Olímpicos vai custar ao clube desportivo 100 euros, mas o clube quer vender as rifas para a viagem de forma a ter 80 euros de lucro. As rifas serão todas vendidas e ao mesmo preço.
A tabela seguinte representa a relação entre o número de rifas (n) que devem vender e o preço (p), em euros, de cada rifa.
- Qual é o número de rifas que deveriam ser vendidas
…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 115 Ex. 8
Enunciado
O Daniel vai abastecer o depósito do seu automóvel. Admite que o número, L, de litros de gasolina que o Daniel introduz no depósito em t minutos é dado por \(L = 33\,t\).
- O depósito do automóvel do Daniel tem 71 litros de capacidade. Quando o Daniel vai abastecer o depósito, o computador de bordo indica que o depósito ainda tem 5 litros de gasolina. Quantos minutos vai demorar o Daniel a encher o depósito, se
…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 115 Ex. 7
Enunciado
Uma Associação de Estudantes vai organizar uma festa num recinto fechado e resolveu, por questões de segurança, que o número de bilhetes a imprimir deveria ser menos 20% do que o número máximo de pessoas que cabem no recinto.
- A Associação de Estudantes decidiu organizar a festa no ginásio da escola onde cabem, no máximo, 300 pessoas. Quantos bilhetes deve a Associação de Estudantes mandar imprimir?
Apresenta os cálculos que efetuares.
- Sendo n o número máximo de
…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 115 Ex. 6
Enunciado
Sabemos que, se exercermos pressão sobre o êmbolo de uma seringa tapando o orifício com o dedo de modo a não deixar sair o gás, o volume diminui à medida que a pressão aumenta. À temperatura de 0 °C registaram-se os valores da tabela.
- O volume, à temperatura de 0 °C, é inversamente proporcional à pressão sobre ele exercida? Porquê?
- Escreve uma expressão que permita obter v em função de p.
- Determina o volume de gás
…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 115 Ex. 5
Enunciado
O Sr. António percebeu que o tempo, t (em horas), gasto para ir da sua cidade para a cidade onde morava o seu irmão, pelo mesmo caminho, dependia da velocidade média, v (em km/h), do seu automóvel.
- Qual é a distância percorrida pelo Sr. António, quando vai visitar o irmão, seguindo aquele caminho?
- Existe proporcionalidade entre as grandezas v e t?
Explica a tua resposta.
- Escreve uma expressão algébrica que relacione o tempo gasto, t,
…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 114 Ex. 3
Enunciado
Copia e completa a tabela, sabendo que m e n são grandezas inversamente proporcionais.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 113 Ex. 9
Enunciado
Na figura, estão representados, num referencial cartesiano, parte do gráfico de uma função quadrática f e o triângulo [OAB].
Sabe-se que:
- o ponto O é a origem do referencial;
- o ponto A pertence ao gráfico da função f e tem abcissa igual a 2;
- o ponto B pertence ao eixo das ordenadas;
- o triângulo [OAB] é retângulo em B;
- a função f é definida por \(f\left( x \right) = a{x^2}\), sendo a
…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 113 Ex. 8
Enunciado
Resolve graficamente as equações seguintes.
- \(2{x^2} + 5x – 3 = 0\)
- \( – {x^2} – 4x + 5 = 0\)
- \(4{x^2} – 2x – 2 = 0\)
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 113 Ex. 7
Enunciado
Considera as funções f e g, definidas por \(f\left( x \right) = {x^2}\) e \(g\left( x \right) = – 6x – 8\).
Determina analiticamente as coordenadas dos pontos de interseção dos gráficos de f e g.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 113 Ex. 6
Enunciado
No referencial cartesiano da figura estão representados os gráficos de duas funções f e g, respetivamente, a parábola de vértice \(\left( {0,\;0} \right)\) que passa pelo ponto \(A\left( { – 1,\; – 1} \right)\) e a reta DE em que \(D\left( {0,\; – 2} \right)\) e \(E\left( {2,\;0} \right)\).
- Determina uma expressão algébrica para cada uma das funções.
- Determina as coordenadas dos pontos de interseção dos dois gráficos.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 113 Ex. 5
Enunciado
Seja f uma função quadrática do tipo \(y = a{x^2}\), com \(a \ne 0\), tal que \(f\left( 1 \right) = – 7\).
Escreve uma expressão algébrica da função f.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 112 Ex. 4
Enunciado
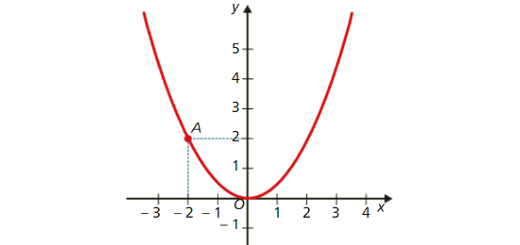
A função g está representada graficamente no referencial cartesiano da figura por uma parábola de eixo vertical e que passa na origem.
O ponto \(A\left( { – 2,\;2} \right)\) pertence ao gráfico de g.
Determina uma expressão algébrica de g.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 112 Ex. 3
Enunciado
Num referencial estão representas as funções f, g, h e j, que são, respetivamente, uma função quadrática, uma função afim, uma função de proporcionalidade direta e uma função constante.
- Define as funções f, g, h e j recorrendo a expressões algébricas.
- Determina os valores de x tais que:
- \(g\left( x \right) = j\left( x \right)\)
- \(f\left( x \right) = h\left( x \right)\)
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 112 Ex. 2
Enunciado
No referencial seguinte estão representados os gráficos de duas funções quadráticas do tipo \(y = a{x^2}\), com a inteiro e diferente de zero.
Escreve as suas expressões algébricas.
Resolução >>
Resolução
<< Enunciado…
Ler mais