Uma função quadrática representada graficamente
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 110 Tarefa 7
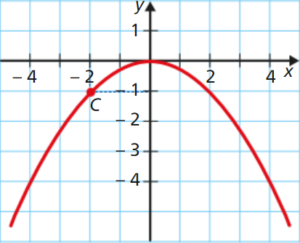Considera uma função f quadrática representada graficamente no referencial cartesiano da figura por uma parábola de eixo vertical e que passa na origem.
Sabendo que o ponto de coordenadas \(\left( { – 2,\; – 1} \right)\) pertence ao gráfico de f, determina a expressão algébrica de f.
Os gráficos das funções do tipo \(f\left( x \right) = a{x^2}\), com \(a \ne 0\), são parábolas de eixo vertical e vértice na origem.
Como o ponto de coordenadas \(\left( { – 2,\; – 1} \right)\) pertence ao gráfico de f, então as suas coordenadas têm de verificar \(f\left( x \right) = a{x^2}\), com \(a \ne 0\).
Assim, vem:
\[\begin{array}{*{20}{l}}{f\left( { – 2} \right) = – 1}& \Leftrightarrow &{a \times {{\left( { – 2} \right)}^2} = – 1}\\{}& \Leftrightarrow &{4a = – 1}\\{}& \Leftrightarrow &{a = – \frac{1}{4}}\end{array}\]
Portanto, a função f pode ser definida por \(f\left( x \right) = – \frac{1}{4}{x^2}\).
