Monthly Archive: Dezembro 2022
Isometrias: Matematicamente Falando 8 - Pág. 102 Ex. 2
Enunciado
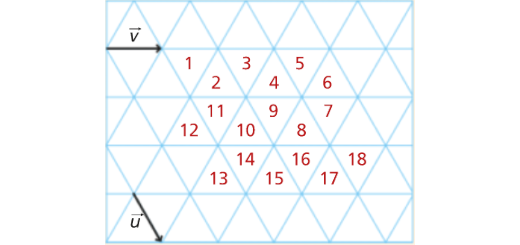
Na figura, os triângulos numerados são todos iguais e equiláteros.
- Caracteriza:
a) uma rotação, uma translação e uma reflexão axial que transformem o triângulo 4 no triângulo 6;
b) duas isometrias diferentes que transformem o triângulo 9 no triângulo 8.
- Relaciona com \({\vec u}\) e \({\vec v}\) o vetor da translação que transforma:
a) o triângulo 9 no triângulo 18;
b) o triângulo 3 no triângulo 16;
c) o triângulo 16 no triângulo 1.
Resolução >>
Resolução… Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 102 Ex. 1
Enunciado
Efetuando uma rotação de amplitude 270°, no sentido negativo, do ponteiro dos minutos, em torno do ponto O, qual será a hora marcada?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 98 Tarefa 10
Enunciado
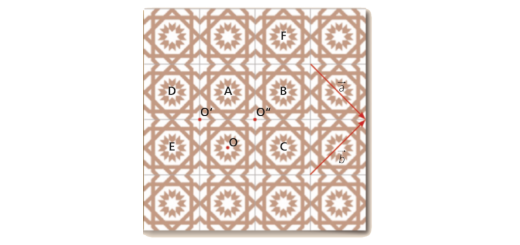
Observa os mosaicos e os vetores \({\vec a}\) e \({\vec b}\).
- Relaciona com \({\vec a}\) e \({\vec b}\) o vetor que define a translação que transforma:
a) a figura A na F;
b) a figura A na E;
c) a figura E na C.
- Indica o centro e a amplitude de rotações que transformem:
a) a figura A na E;
b) a figura B na C.
- Qual é o transformado pela reflexão axial de eixo O’O”:
a)
…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 97 Ex. 4
Enunciado
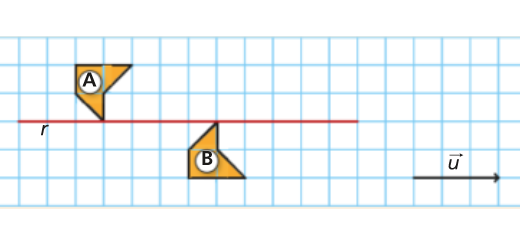
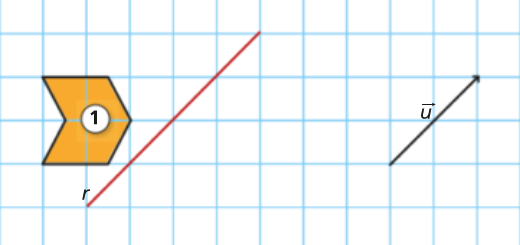
Na figura, está representada uma grelha quadriculada onde foram desenhados dois pentágonos iguais, A e B, uma reta \(r\) e um vetor \({\vec u}\), com a mesma direção da reta \(r\).
- Determina a imagem \(A’\), do pentágono \(A\), pela reflexão deslizante de eixo \(r\) e de vetor \({\vec u}\) e, depois, determina a imagem \({A^{”}}\), do pentágono \(A’\), pela mesma reflexão deslizante.
- Identifica uma isometria (reflexão axial, rotação, translação ou reflexão deslizante) que transforme o pentágono \(A\)
…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 97 Ex. 3
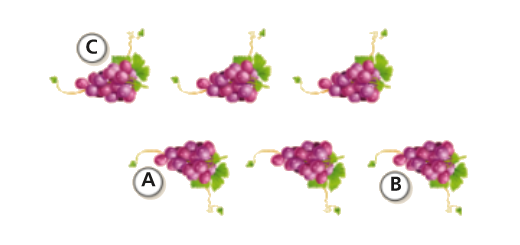
Considerando o cacho de uvas como motivo, indica a ou as isometrias necessárias para obter as figuras B e C a partir de A, nos seguintes padrões.
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 97 Ex. 2
Enunciado
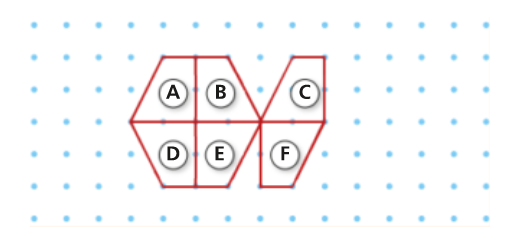
A figura seguinte é constituída por seis trapézios iguais.
Identifica a isometria que transforma:
- a figura A na figura B;
- a figura A na figura C;
- a figura B na figura F;
- a figura B na figura D;
- a figura B na figura E;
- a figura E na figura F;
- a figura C na figura D.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 97 Ex. 1
Enunciado
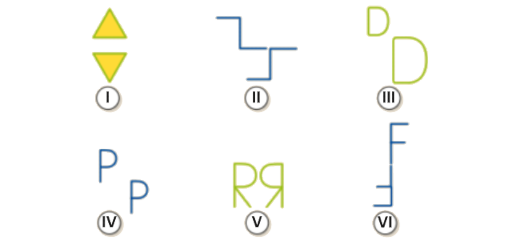
Observa as figuras.
- Existe um único par de figuras que podem ser relacionadas por meio de uma translação. Identifica-o.
- Existem dois pares de figuras que são obtidas por uma reflexão axial. Quais são?
- Quais são os pares de figuras que são obtidas através de uma meia-volta?
- Há algum par de figuras obtido através de uma reflexão deslizante? Qual é?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 96 Tarefa 9
Enunciado
Copia a figura 1, a reta e o vetor \({\vec u}\).
- Obtém a figura 2, que é a imagem da figura 1 pela reflexão de eixo \(r\).
- Desenha a figura 3, que é o transformado da figura 2 pela translação de vetor \({\vec u}\).
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 95 Ex. 2
Enunciado
A figura abaixo representa motivos de decoração de um tapete.
Sabendo que \(\vec u = \overrightarrow {AB} \) e \(\vec v = \overrightarrow {BC} \), determina a imagem de:
- \(A\) por \({T_{\vec v}}\)
- \(B\) por \({T_{ – \vec u}}\)
- \(D\) pela translação compostas das translações \({T_{\vec u}}\) e \({T_{ – \vec v}}\)
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 95 Ex. 1
Enunciado
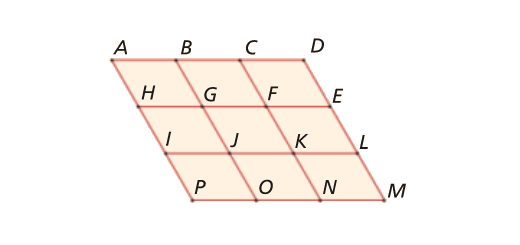
Na figura estão representados nove paralelogramos iguais.
Copia e completa, usando as letras da figura, cada uma das seguintes igualdades.
- \(F + \overrightarrow {DL} = \ldots \)
- \( \ldots + \overrightarrow {ML} = H\)
- \(O + \ldots = N\)
- \(\overrightarrow {JK} + \overrightarrow {EC} = \ldots \)
- \(\overrightarrow {PJ} + \overrightarrow {FE} + \overrightarrow {CF} = \ldots + \overrightarrow {CF} = \ldots \)
- \(\overrightarrow {HG} + \overrightarrow {OK} + \overrightarrow {DL} = \overrightarrow {HG} + \ldots =
…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 94 Tarefa 8
Enunciado
Considera os vetores \({\vec u}\), \({\vec v}\) e \({\vec w}\).
- Copia os vetores para o teu caderno.
- Desenha e compara os vetores \(\vec a = \vec u + \vec v\) e \(\vec b = \vec v + \vec u\).
- Determina o vetor \(\vec c = \vec v + \vec w\).
- Desenha e compara os vetores \(\vec d = \vec a + \vec w\) e \(\vec f = \vec u + \vec c\).
- Desenha o vetor \(\vec g
…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 93 Ex. 4
Enunciado
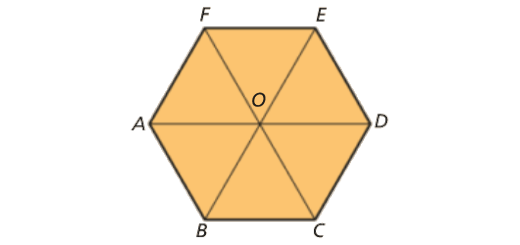
A figura representa um hexágono regular dividido em seis triângulos geometricamente iguais.
Usando letras da figura, determina:
- \(\overrightarrow {BC} + \overrightarrow {BO} \)
- \(\overrightarrow {OD} + \overrightarrow {BC} \)
- \(\overrightarrow {AB} + \overrightarrow {CF} \)
- \(\overrightarrow {DE} + \overrightarrow {FO} \)
- \(B + \overrightarrow {OE} \)
- \({T_{\overrightarrow {EF} }}\left( O \right)\)
- \(\left( {{T_{\overrightarrow {AF} }} \circ {T_{\overrightarrow {FO} }}} \right)\left( A \right)\)
- \(E + \overrightarrow {AB} \)
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 93 Ex. 3
Enunciado
Determina \(\vec a + \vec b\) em cada caso.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 93 Ex. 2
Enunciado
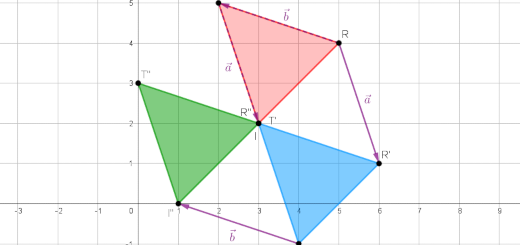
Considera o triângulo [TRI] cujas coordenadas são \(T\left( {2,5} \right)\), \(R\left( {5,4} \right)\), \(I\left( {3,2} \right)\) e os vetores \(\vec a = \overrightarrow {TI} \) e \(\vec b = \overrightarrow {RT} \).
- Desenha o triângulo [TRI] num sistema de eixos cartesianos.
- Aplica ao triângulo [TRI] a translação de vetor \(\vec a = \overrightarrow {TI} \).
Designa o novo triângulo por [T’R’I’].
- Aplica ao triângulo [T’R’I’ a translação de vetor \(\vec b = \overrightarrow {RT} \).
Designa o
…
Ler mais