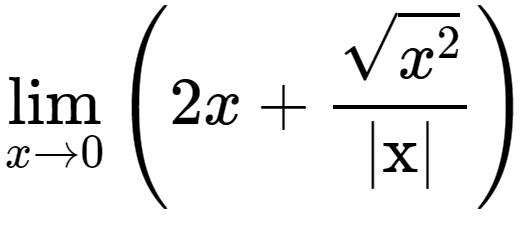A Casinha da Matemática

A Álgebra é generosa; ela frequentemente dá mais do que aquilo que lhe é pedido. (D'Alembert)

A Casinha da Matemática Blog

0

Aplicando / 12.º Ano / Teoria de limites

Dadas as funções reais de variável real

Teoria de limites: Infinito 12 A - Parte 2 Pág. 207 Ex. 21

Enunciado

Dadas as funções reais de variável real, assim definidas:$$\begin{array}{*{20}{c}}
{f(x) = {x^2} + 1}&{\text{e}}&{g(x) = \frac{1}{x}}
\end{array}$$

  1. Determine, em função de $h$, a taxa média de variação de cada uma das funções no intervalo $\left[ {1,1 + h} \right]$, com $h > 0$.
  2. Calcule se existir:

    a) $\mathop {\lim }\limits_{h \to 0} \frac{{f(1 + h) – f(1)}}{h}$
    ­
    b) $\mathop {\lim }\limits_{h \to 0} \frac{{g(1 + h) – g(1)}}{h}$
    ­
    c) $\mathop {\lim }\limits_{h \to 0} \frac{{f(a

… Ler mais
0

Ciência e Tecnologia / Astronomia

ABC da Astronomia | Meteoro

Admirados por uns e muito temidos por outros, eles são meteoróides antes de chegar à Terra e passam a ser chamados de meteoros quando riscam nossa atmosfera. Depois disso, quando são grandes e chegam até o chão, são meteoritos. Neste ABC da Astronomia você vai descobrir que o Meteoro é um acontecimento, e não um objeto. Entenda também a diferença entre eles e as estrelas cadentes. Ah! Também falamos das chuvas de meteoros nesse episódio. O ABC da Astronomia é … Ler mais

0

12.º Ano / Teoria de limites / Aplicando

Calcule os seguintes limites, se existirem

Teoria de limites: Infinito 12 A - Parte 2 Pág. 206 Ex. 20
Enunciado

Calcule os seguintes limites, se existirem:

  1. ${\mathop {\lim }\limits_{x \to 3} \frac{{{x^2} – 4x + 3}}{{x + 1}}}$
    ­
  2. ${\mathop {\lim }\limits_{x \to  – 1} \frac{x}{{{{\left( {x + 1} \right)}^2}}}}$
    ­
  3. ${\mathop {\lim }\limits_{t \to  – \infty } \left( {2{t^3} + {t^2} + 1} \right)}$
    ­
  4. ${\mathop {\lim }\limits_{m \to  – 1} \frac{{{m^3} + 1}}{{m + 1}}}$
    ­
  5. ${\mathop {\lim }\limits_{r \to 2} \frac{{{r^4} – 16}}{{r – 2}}}$
    ­
  6. $\mathop {\lim }\limits_{x \to 3} \frac{{\left| { –
… Ler mais
0

Aplicando / 12.º Ano / Teoria de limites

Limites laterais da função $f$

Teoria de limites: Infinito 12 A - Parte 2 Pág. 204 Ex. 14
Enunciado

Sabe-se que $f({u_n}) = 2$ e $f({v_n}) =  – 2$ para todas as sucessões $({u_n})$ e $({v_n})$ nas condições seguintes:

  • $\begin{array}{*{20}{l}}   {({u_n} \in {D_f}}& \wedge &{{u_n} > 3,}&{\forall n \in \mathbb{N})}& \wedge &{{u_n} \to 3} \end{array}$
  • $\begin{array}{*{20}{l}}   {({v_n} \in {D_f}}& \wedge &{{v_n} < 3,}&{\forall n \in \mathbb{N})}& \wedge &{{v_n} \to 3} \end{array}$

Conclua, caso seja possível, quanto à existência e ao valor:

  1. dos limites laterais da função $f$ no ponto de abcissa 3;
  2. do limite da função
… Ler mais
0

Aplicando / 9.º Ano / Circunferência e polígonos

Completa a tabela

Circunferência e plígonos: Matematicamente Falando 9 - Pág. 37 Ex. 3
Enunciado

Os círculos seguintes têm de raio 5 cm.

Completa a tabela:
Arco AB Arco CD Arco EF
Ângulo ao centro
Fração do círculo
Comprimento do arco
Área do setor circular

Resolução >> Resolução

<< Enunciado… Ler mais