Um hexágono regular
Circunferência e plígonos: Matematicamente Falando 9 - Pág. 37 Ex.2
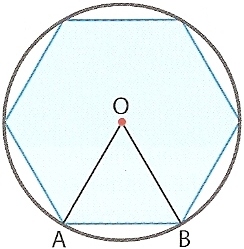 A figura ao lado é um hexágono regular.
A figura ao lado é um hexágono regular.
Calcula a sua área, sabendo que o raio da circunferência é 4 cm.
 Comecemos por provar que o triângulo [AOB] é equilátero:
Comecemos por provar que o triângulo [AOB] é equilátero:
[OA] e [OB] são raios da mesma circunferência, logo o triângulo [AOB] é isósceles.
Num triângulo, a lados geometricamente iguais opõem-se ângulos geometricamente iguais. Logo, os ângulos OAB e OBA são geometricamente iguais.
Como a amplitude do ângulo ao centro AOB é 60º, pois é igual à amplitude de cada um dos 6 arcos geometricamente iguais em que a circunferência foi dividida, resulta que os três ângulos internos do triângulo [AOB] são geometricamente iguais.
Sendo equiângulo, o triângulo [AOB] é equilátero.
Calculemos agora o apótema:
Aplicando o teorema de Pitágoras no triângulo retângulo [AOM], temos:
$$\begin{array}{*{20}{l}}
{\overline {OM} }& = &{\sqrt {{{\overline {AO} }^2} – {{\overline {AM} }^2}} } \\
{}& = &{\sqrt {{4^2} – {2^2}} } \\
{}& = &{\sqrt {12} } \\
{}& = &{2\sqrt 3 }
\end{array}$$
Assim, a área do triângulo [AOB] é:
$$\begin{array}{*{20}{l}}
{{A_{[AOB]}}}& = &{\frac{{\overline {AB} \times \overline {OM} }}{2}} \\
{}& = &{\frac{{4 \times 2\sqrt 3 }}{2}} \\
{}& = &{4\sqrt 3 \,\,c{m^2}}
\end{array}$$
Logo, a área do hexágono é:
$$\begin{array}{*{20}{l}}
A& = &{6 \times {A_{[AOB]}}} \\
{}& = &{6 \times 4\sqrt 3 } \\
{}& = &{24\sqrt 3 \,\,c{m^2}}
\end{array}$$