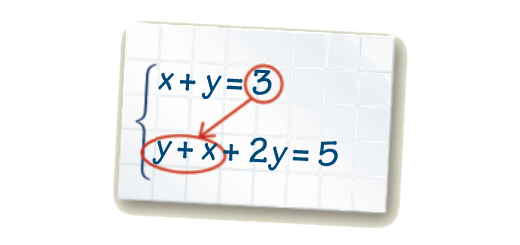A Casinha da Matemática Blog
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 204 Ex. 10
Enunciado
Completa o sistema de equações seguinte de modo que a sua solução seja \(\left( {12, – 7} \right)\).
\[\left\{ {\begin{array}{*{20}{l}}{2x + y = \ldots }\\{3x – 2y = \ldots }\end{array}} \right.\]
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 204 Ex. 9
Enunciado
Considera o seguinte sistema de equações: \[\left\{ {\begin{array}{*{20}{l}}{x + 3y = 11}\\{5y – 68 = 3\left( {x – 1} \right)}\end{array}} \right.\]
Qual dos quatro pares ordenados (x, y) que se seguem é a solução deste sistema?
[A] \(\left( {\frac{{50}}{7}, – \frac{{73}}{7}} \right)\) [B] \(\left( { – \frac{{73}}{7},\frac{{50}}{7}} \right)\) [C] \(\left( {7, – 10} \right)\) [D] \(\left( { – 10,7} \right)\)
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 204 Ex. 8
Enunciado
Resolve os seguintes sistemas de equações.
\(\left\{ {\begin{array}{*{20}{l}}{2\left( {x – 1} \right) – 4y = 1}\\{3y = 2}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{2x + 3y = 10}\\{4x – y = – 1}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{x + y = 7}\\{\frac{{2x}}{5} = \frac{{3y}}{7}}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{5\left( {x + 1} \right) + 3\left( {y – 2} \right) = 4}\\{8\left( {x + 1} \right) + 5\left( {y – 2} \right) = 9}\end{array}} \right.\)
Resolução >>
Resolução
<< Enunciado…
Ler mais
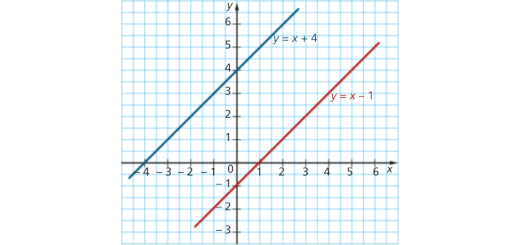
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 203 Ex. 7
Enunciado
Observa a representação gráfica de um sistema de equações.
- Qual é a posição relativa das retas representadas?
- Classifica o sistema de equações. Justifica a tua resposta.
Resolução >>
Resolução
<< Enunciado…
Ler mais
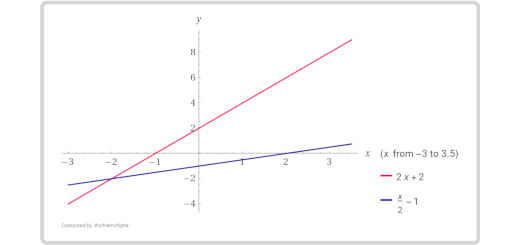
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 203 Ex. 6
Enunciado
Representa graficamente e classifica cada sistema de equações.
\(\left\{ {\begin{array}{*{20}{l}}{y = x – 7}\\{x = y + 3}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{y = 2x + 2}\\{x = 2y + 2}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{y = x + 2}\\{x = y – 2}\end{array}} \right.\)
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 203 Ex. 5
Enunciado
A pressão sanguínea normal, P, de uma pessoa saudável pode ser estimada mediante a expressão \[P = 11 + \frac{E}{{20}}\] onde E representa a idade em anos.
- Estima a pressão sanguínea normal estimada aos 30, 50 e 70 anos.
- Escreve uma expressão que te permita estimar a idade, conhecendo a pressão sanguínea.
- Se uma pessoa tem uma pressão sanguínea de 14, qual esperas que seja a sua idade?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 203 Ex. 4
Enunciado
Num livro antigo de medicina aparece a fórmula \[C = \frac{{A \times i}}{{i + 12}}\] sendo C a dose de um medicamento para crianças (em mg), A a dose para adultos (em mg) e i é a idade (em anos) da criança. Esta fórmula só se pode aplicar a crianças com mais de um ano de idade.
- Qual é a dose para uma criança de 6 anos, se a dose de adulto é de 15 mg?
- Uma
…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 203 Ex. 3
Enunciado
A equação \[e = vt\] relaciona o espaço e percorrido por um móvel, em movimento retilíneo e uniforme, à velocidade v, durante o período de tempo t.
Resolve a equação em ordem a t.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 203 Ex. 2
Enunciado
Um retângulo tem de perímetro 10 cm.
- Escreve uma expressão que traduza o enunciado.
- Determina todas as soluções inteiras da equação escrita em 1.
- Se a largura for um quarto do comprimento, quais são as dimensões do retângulo?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 203 Ex. 1
Enunciado
Considera a equação: \(\frac{3}{2}x + 2y = 3\)
- O par \(\left( {2, – 1} \right)\) é solução?
- Resolve a equação em ordem a y.
- Procura o valor de y para \(x = – 4\).
- Qual é o valor de x para \(y = 0\)?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 202 Ex. 5
Enunciado
Escreve na forma canónica os seguintes sistemas e, em seguida, resolve-os, utilizando o método de substituição.
\(\left\{ {\begin{array}{*{20}{l}}{x – 3y = 4 + x}\\{2\left( {x – 3} \right) = 3\left( {y – 1} \right)}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{3\left( {x + y} \right) – 2 = x}\\{y = 5 – x}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{\frac{p}{2} + \frac{q}{3} – 4 = 0}\\{\frac{p}{4} – \frac{q}{2} + 2 = 0}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{3\left( {a – 2} \right) = \frac{1}{2}a + b}\\{a – 2b
…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 202 Ex. 4
Enunciado
Ao resolver um sistema de equações, a Rita percebeu que podia fazer uma substituição especial.
Observa o que ela escreveu.
Resolve o sistema, aproveitando a ideia da Rita.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 202 Ex. 3
Enunciado
Considera o seguinte problema:
- Escreve uma equação do 1.º grau que permita completar o sistema que se segue, de modo que este traduza o problema.
\[\left\{ {\begin{array}{*{20}{l}}{x = y + 3}\\ \cdots \end{array}} \right.\]
- Que resposta darias a este problema?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 202 Ex. 2
Enunciado
Considera o seguinte sistema de equações.
\[\left\{ {\begin{array}{*{20}{l}}{x – y = 6}\\{3x – \frac{y}{2} = 3}\end{array}} \right.\]
Qual dos pares ordenados (x,y) seguintes é solução do sistema?
[A] \(\left( {0,6} \right)\) [B] \(\left( {0, – 6} \right)\) [C] \(\left( { – 6,0} \right)\) [D] \(\left( {12,6} \right)\)
Resolução >>
Resolução
<< Enunciado…
Ler mais