A Casinha da Matemática Blog
Análise combinatória: Infinito 12 A - Parte 1 Pág. 173 Ex. 39
Enunciado
Um fabricante de bicicletas atribui um código de fabrico a cada bicicleta que produz.
Cada código é formado por quatro algarismos (de 0 a 9) colocados por uma certa ordem.
Escolhida uma bicicleta ao acaso, qual a probabilidade do seu código ter exatamente três zeros?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Enunciado
Para planear a apanha da uva, na quinta de Alzubar, construi-se a seguinte tabela:
| Número de trabalhadores ($t$) |
100 |
50 |
25 |
| Número de dias que leva a apanha da uva ($d$) |
1 |
2 |
4 |
Na tabela, as variáveis $t$ e $d$ referem-se a grandezas inversamente proporcionais.
- Quando o número de trabalhadores aumenta, o que acontece ao número de dias que leva a apanha da fruta?
- Determina a constante de proporcionalidade inversa.
- Neste caso, o que representa a
…
Ler mais
Proporcionalidade inversa: Matematicamente Falando 9 - Parte 1 Pág. 69 Ex. 4
Enunciado
Um comboio, que viaja à velocidade média de 75 km/h, faz um certo percurso em 36 minutos.
Quanto tempo demoraria a fazer o mesmo percurso, se andasse a uma velocidade média de 45 km/h?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa: Matematicamente Falando 9 - Parte 1 Pág. 69 Ex. 3
Enunciado
Sabemos que, se exercermos pressão sobre o êmbolo de uma seringa tapando o orifício com o dedo de modo a não deixar sair o ar, o volume diminui à medida que a pressão aumenta.
À temperatura de 0 ºC registaram-se os seguintes valores:
| Pressão $p$ (em atmosferas) |
224 |
89,6 |
44,8 |
22,4 |
11,2 |
5,6 |
2,24 |
0,448 |
| Volume $v$ (em litros) |
0,1 |
0,25 |
0,5 |
1 |
2 |
4 |
10 |
50 |
- Que acontece ao volume se a pressão aumenta? E se
…
Ler mais
Função de proporcionaldade inversa
Enunciado
| Base ($x$) |
Altura ($y$) |
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
Pretende-se construir retângulos diferentes, mas todos de área 36 unidades.
- Completa a tabela, com os comprimentos adequados para a altura.
- Se aumentarmos o comprimento da base, o que acontece ao comprimento da altura?
- Se duplicarmos o comprimento da base, o que acontece ao comprimento da altura? E se o triplicarmos?
- Multiplica os valores correspondentes das variáveis $x$ e $y$. O que obténs?
- Representa graficamente y em função
…
Ler mais
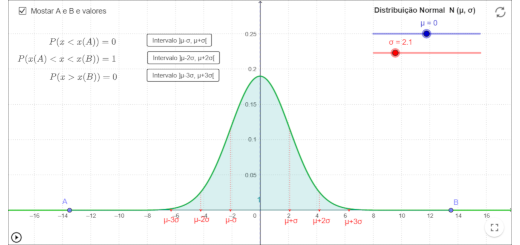
A curva de Gauss – curva da distribuição normal mediante a qual é possível representar-se medidas prováveis da Estatística
Distribuição normal
A distribuição normal é uma das mais importantes distribuições da estatística, conhecida também como Distribuição de Gauss ou Gaussiana. Foi primeiramente introduzida pelo matemático Abraham de Moivre.
Além de descrever uma série de fenómenos físicos e financeiros, possui grande uso na estatística inferencial. É inteiramente descrita por seus parâmetros de média e desvio padrão, ou seja, conhecendo-se estes consegue-se determinar qualquer probabilidade em uma distribuição Normal.
Um interessante uso da Distribuição Normal … Ler mais
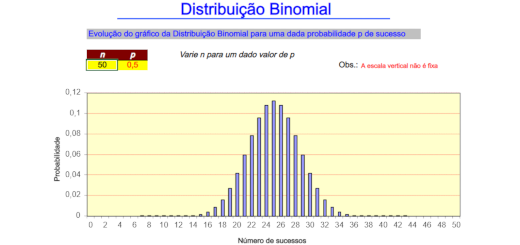
Distribuição binomial
Plinko I
Plinko and the Binomial Distribution
A Bernoulli trial is an experiment that results in a success with probability $p$ and a failure with probability $1-p$. A random variable is said to have a Binomial Distribution if it is the result of recording the number of successes in n independent Bernoulli trials.
In the Applet below, we have represented repeated independent Bernoulli trials by a single ball falling through an array of pins. Each time … Ler mais
9.º Ano: Proporcionalidade inversa; Representações gráficas
A presente Ficha de Trabalho aborda o tema Proporcionalidade inversa; Representações gráficas.
As dificuldades que encontres durante a sua resolução deves tentar superá-las consultando o manual e o caderno diário; depois, poderás tirar as dúvidas na aula ou na sala de estudo.
Distribuição normal: Infinito 12 A - Parte 1 Pág. 173 Ex. 38
Enunciado
Os resultados obtidos pelos alunos a uma certa disciplina distribuem-se segundo $N\left( {12;\;2,5} \right)$.
- Qual a probabilidade de, escolhendo um destes alunos ao acaso, a sua nota não ser superior a 7?
- Qual a classificação mínima que um aluno deve ter para se situar entre os 2,5% dos alunos com melhores notas?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distribuição normal: Infinito 12 A - Parte 1 Pág. 173 Ex. 37
Enunciado
Os pesos, em kg, de 600 alunos do ensino secundário distribuem-se segundo N(60, 5).
Calcule, aproximadamente, quantos deles têm peso:
- pertencente ao intervalo ]55, 65[;
- pertencente ao intervalo ]50, 70[;
- superior a 60 kg,
- inferior a 70 kg.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distribuição normal: Infinito 12 A - Parte 1 Pág. 173 Ex. 35
Enunciado
A distribuição de alturas de 2000 pessoas de uma região é representada por uma curva normal N (162, 7).
Indique um valor aproximado da percentagem daqueles cuja altura:
- ultrapassa 162 cm;
- está compreendida entre 155 cm e 169 cm;
- é menor que 155 cm;
- é maior que 176 cm.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Esperança matemática e desvio padrão: Infinito 12 A - Parte 1 Pág. 172 Ex. 34
Enunciado
Numa fábrica de material elétrico, recolheu-se uma amostra de 400 lâmpadas, para estudar o seu tempo de duração.
| Horas de vida |
200 a 399 |
400 a 599 |
600 a 799 |
| N.º de lâmpadas |
48 |
203 |
149 |
- Construa um histograma e calcule a esperança matemática e o desvio padrão da distribuição.
- Qual a percentagem de lâmpadas que duram menos do que $\mu -2\sigma $?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distribuição de probabilidades: Infinito 12 A - Parte 1 Pág. 172 Ex. 33
Enunciado
A lei de probabilidade de uma variável aleatória $X$ é:
| ${{x}_{i}}$ |
1 |
2 |
3 |
4 |
5 |
6 |
| $P(X={{x}_{i}})$ |
0,1 |
0,2 |
0,1 |
0,3 |
0,1 |
0,2 |
- Calcule a esperança matemática e o desvio padrão de $X$.
- Uma variável aleatória $Y$ toma os valores 3, 4, 5 e 6.
a) Qual é a lei de probabilidade de $Y$, sabendo que:
$P(Y>5)=0,5$; $P(Y<5)=\frac{1}{3}$ e $P(Y=3)=P(Y=4)$.
b) Qual é a esperança matemática e o desvio padrão de $Y$?
Resolução >>
Resolução
<< …
Ler mais
Distribuição de probabilidades: Infinito 12 A - Parte 1 Pág. 172 Ex. 32
Enunciado
Um fabricante analisou os registos diários do número de artigos vendidos por um dos seus representantes e elaborou a seguinte distribuição de probabilidades:
| ${{x}_{i}}$ – N.º de artigos vendidos |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| $P(X={{x}_{i}})$ |
0,1 |
0,35 |
0,3 |
0,1 |
$p$ |
0,07 |
0,06 |
- Calcule o valor de $p$.
- Sendo $\mu $ o valor médio e $\sigma $ o desvio padrão da distribuição, qual é a probabilidade do número de vendas pertencer ao intervalo \[\left] \mu -\sigma
…
Ler mais






















![Observa o triângulo [ABC], retângulo em A](https://www.acasinhadamatematica.pt/wp-content/uploads/2018/03/9V2Pag056-5a-720x340.png)




