Distribuição normal

Abraham De Moivre

A distribuição normal é uma das mais importantes distribuições da estatística, conhecida também como Distribuição de Gauss ou Gaussiana. Foi primeiramente introduzida pelo matemático Abraham de Moivre.

Além de descrever uma série de fenómenos físicos e financeiros, possui grande uso na estatística inferencial. É inteiramente descrita por seus parâmetros de média e desvio padrão, ou seja, conhecendo-se estes consegue-se determinar qualquer probabilidade em uma distribuição Normal.

Um interessante uso da Distribuição Normal é que ela serve de aproximação para o cálculo de outras distribuições quando o número de observações fica grande. Essa importante propriedade provém do Teorema Central do Limite que diz que “toda soma de variáveis aleatórias independentes de média finita e variância limitada é aproximadamente Normal, desde que o número de termos da soma seja suficientemente grande” (ver o teorema para um enunciado mais preciso).

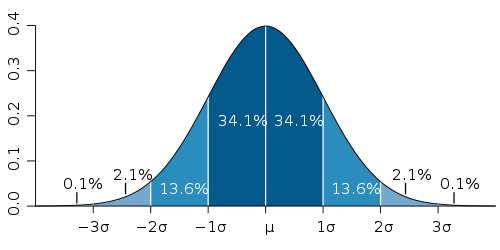A área em azul escuro está a menos de um desvio padrão (σ) da média. Em uma distribuição normal, isto representa cerca de 68% do conjunto, enquanto dois desvios padrões desde a média (azul médio e escuro) representam cerca de 95%, e três desvios padrões (azul claro, médio e escuro) cobrem cerca de 99.7%.

• Distribuição normal (Wikipédia)

• West Virgínia University